티스토리 뷰
(2)MergeSort
이 챕터에서는 Sorting의 대표적인 한 방법인 MergeSort에 대해 다루며 그 수행 시간을 분석해본다.
MergeSort는 기본적으로 다음과 같은 아이디어에서 시작한다.
이미 정렬되어 있는 두 개의 배열 L[1,...,l]과 R[1,.....,r]이 있다고 해보자. 이 때 L과R 배열을 병합하여 새로운 배열A'을 만든다고 하면, 어떻게 하면 A'을 정렬된 배열로 병합할 수 있을까?
우선 처음A[1]을 생각해보자, 그러면 A[1]에 들어가야 할 원소는 L과 R의 원소를 합쳐놓은 집합에서 제일 작은 원소이다. 이는 L의 최소 원소(L[1])와 R의 최소 원소(R[1])중 더 작은 원소와 같으므로 min(L[1], R[1])이 된다. L[1]이 더 작은 상황이라고 가정해보면 A[1]에 L[1]이 들어가면 된다. 그럼 이제 남은 원소들은 L[2,...,l]과 R[1,...r]이 된다.
이제 A[2]에 넣어야 할 원소를 생각해보자. A[2]에 들어가야 하는 원소는 정렬된 배열이라는 특성 상 다음과 같은 조건을 만족해야 한다.
(i) A[1]보다 크거나 같다.
(ii) (i)을 만족하는 모든 원소들 중에서 가장 작다.
이 때 L[2,...,l]과 R[1,....,r]들은 모두 (i)을 기본적으로 만족한다. 왜냐하면 A[1]==L[1]은 L[2,...,l]보다 작거나 같고 L[1]은 R[1,...,r]보다 작거나 같기 때문. 따라서 (i)에 대한 걱정없이 (ii)를 고려하면 된다.
이제 남은 원소들은 L[2,...,l]과 R[1,....,r]고 A[1]의 선정과 마찬가지로 L[2]와 R[1]을 비교하여 최소인 원소를 선정하면 된다. 이렇게 A를 끝까지 채워나간다. 이 때 L과 R중 한 배열의 원소가 모두 바닥나면 그냥 다른 배열의 모든 남은 원소들을 갖다가 A에 순서대로 채우면 된다. 이러한 과정을 Merge(병합)라 하는데, MergeSort는 Merge과정을 핵심적으로 활용하는 정렬이다. 그러면 이 Sorting이 구체적으로 어떤 방법인지 알아보기 전에, 이 MergeSort라는 알고리즘이 속하는 카테고리인 Divide & Conquer에 대해 알아보자.
Divide & Conquer(분할 정복)는 문제를 다음과 같은 아이디어로 푸는 알고리즘을 얘기한다.
(1)Divide: 하나의 큰 문제를 동일한 성질을 가진 작은 subproblem으로 쪼갠다.
(2)Conquer: Divide를 하면서 문제의 크기를 줄이다보면, 자명하거나 쉬운 방법으로 subproblem들이 풀리는 경우가 있다. 이 때 이 subproblem들을 recursive하게 풀어가는 과정을 Conquer라 한다.
(3)Combine: 각 Conquer된 Subproblem들의 해를 병합하여 큰 Problem의 해로 만들어간다.
MergeSort도 이와 같은 과정으로 풀리는 알고리즘을 이야기하는데, 다음<그림1>을 가지고 설명하겠다. (MergeSort는 2가지 유형의 접근이 있는데 <그림1>의 접근은 top-down이다. recursion을 사용하지 않는 botton-up도 가능하다.)
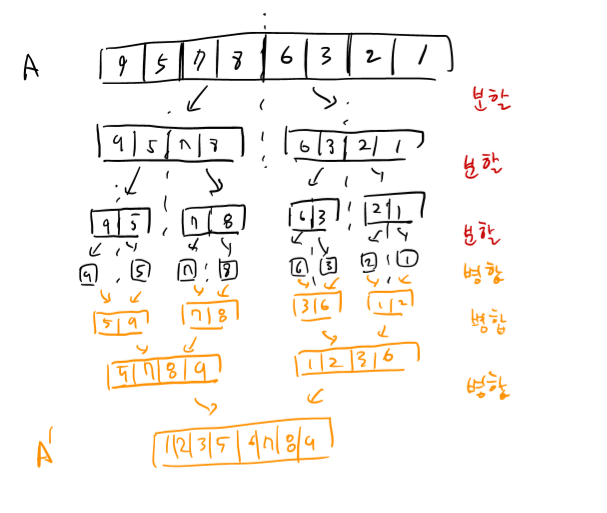
우선 배열을 계속 2개로 쪼개 나간다. 이것은 recursion으로 수행한다. recursion의 basis case는 그 원소가 한 개일 때가 된다. 그 때는 배열을 정렬할 필요가 없다. 분할한 다음에는 위에서 얘기한 병합 step을 계속 밟아가면 된다. 따라서 Divide & Conquer과정을 써보면 다음과 같을 것이다.
(1)Divide: 주어진 배열을 2개로 쪼갠다. 배열의 원소가 한 개면 쪼갤 필요 없다.
(2)Conquer&Combine: 주어진 두 정렬된 배열을 Merge하면 새롭게 정렬된 배열이 나온다.
그럼 이런 정렬 방법에서 Loop Invariant는 무엇인가? 잘 생각해보면 merge시 j'th loop에서 A에 있는 j개의 원소들은 L과 R에서 가장 작은 j개의 원소들이 ascending order로 정렬되어있고 L과 R에 남은 원소들의 제일 첫 원소는 각각의 배열에서 제일 작은 원소여야 한다. 이 Loop invariant또한 Initiallization, Maintanence, Termination관점에서 검증해볼 수 있다.
MERGE과정을 함수로 구현하였다고 하면 MergeSort함수는 다음과 같이 recursive한 함수로 구현할 수 있다.
void Mergesort(int* arr, int start, int end) {
//recursively call
if (start >= end) return; //basis case: need nothing to do
else {
//divide array into two subarrays
int mid = (start + end) / 2;
//Make both sides sorted
Mergesort(arr, start, mid);
Mergesort(arr, mid + 1, end);
//Now, Merge two array
MERGE(arr, start, mid+1,end);
}
}
<코드1: MergeSort>
Merge는 위의 설명을 토대로 L배열과 R배열을 만든 뒤 각 배열에서 index를 움직이며 비교해나간다. 이 때 L과 R의 끝에는 INFINITE를 넣는데, 이는 한 쪽 배열이 끝난 것을 검사하는 과정을 loop에 넣는 것이 너무 비효율적이기 때문이다. 물론 이런 INFINITE의 추가를 위해 L과 R을 따로 만들어줘야하니 메모리의 사용이 조금은 늘어나는 셈이다. <그림1>의 index name을 토대로 <코드2>의 merge를 작성하였다.
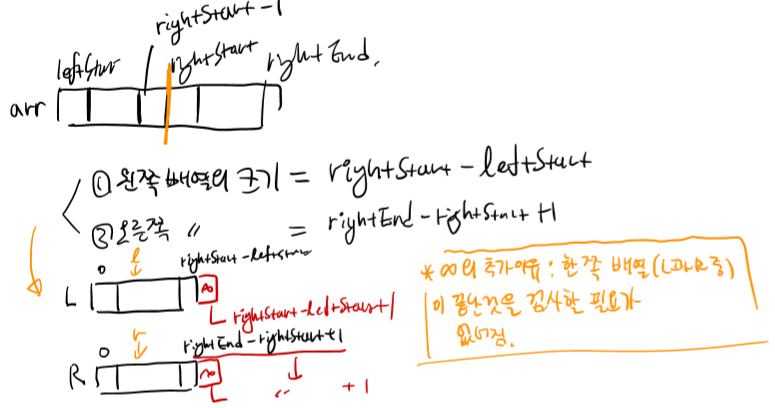
void MERGE(int* arr, int leftStart, int rightStart,int rightEnd) {
int arrsize = rightEnd - leftStart + 1;
//to make it easy and closer to my description, i will define subarray L and R that contain infitinite
//basically don't need to copy
int* L = new int[rightStart - leftStart + 1];
int* R = new int[rightEnd - rightStart + 2];
for (int i = 0; i < rightStart - leftStart; i++)
L[i] = arr[leftStart + i];
L[rightStart - leftStart] = INFINITE;
for (int i = 0; i < rightEnd - rightStart + 1; i++)
R[i] = arr[rightStart + i];
R[rightEnd - rightStart + 1] = INFINITE;
//now Merge
int r = 0;
int l = 0;
for (int i = 0; i < arrsize; i++)
arr[leftStart+i] = (L[l] < R[r]) ? L[l++] : R[r++];
delete[] L;
delete[] R;
}
<코드2: MERGE>
Testcase와 Constant 정의를 포함한 모든 testCode는 다음과 같다.
#include<iostream>
using namespace std;
#define INFINITE 1000000;
void MERGE(int* arr, int leftStart, int rightStart,int rightEnd) {
int arrsize = rightEnd - leftStart + 1;
//to make it easy and closer to my description, i will define subarray L and R that contain infitinite
//basically don't need to copy
int* L = new int[rightStart - leftStart + 1];
int* R = new int[rightEnd - rightStart + 2];
for (int i = 0; i < rightStart - leftStart; i++)
L[i] = arr[leftStart + i];
L[rightStart - leftStart] = INFINITE;
for (int i = 0; i < rightEnd - rightStart + 1; i++)
R[i] = arr[rightStart + i];
R[rightEnd - rightStart + 1] = INFINITE;
//now Merge
int r = 0;
int l = 0;
for (int i = 0; i < arrsize; i++)
arr[leftStart+i] = (L[l] < R[r]) ? L[l++] : R[r++];
delete[] L;
delete[] R;
}
void Mergesort(int* arr, int start, int end) {
//recursively call
if (start >= end) return; //basis case: need nothing to do
else {
int mid = (start + end) / 2;
//Make both sides sorted
Mergesort(arr, start, mid);
Mergesort(arr, mid + 1, end);
//Now, Merge two array
MERGE(arr, start, mid+1,end);
}
}
int main() {
int size = 10;
int arr[] = { 1,5,2,4,3,8,4,7,9,10 };
cout << "before sorting: ";
for (int i = 0; i < size - 1; i++)
cout << arr[i] << " ";
cout << endl;
Mergesort(arr, 0, size-1);
cout << "after sorting: ";
for (int i = 0; i < size - 1; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
<코드3: TestCode>
이런 MergeSort는 우리가 구현한 Top-down방식 외에 bottom-up으로도 구현할 수 있다. 그런데 둘이 핵심 연산인 Merge는 똑같으니까 Top-Down을 했으면 Botton-Up도 도전해볼 만하다.
MergeSort의 시간복잡도 분석은 아래 <그림2>와 같다.

MergeSort의 특징은 다음과 같다.
1. <그림1>을 보면 recursive한 과정에서 각 step에서의 array저장이 필요하므로 배열의 크기에 따라 달라지는 추가적인 메모리를 요구함을 알 수 있다. 즉, insertionsort와 같은 in-place sort가 아니다.
2. 연산 수행시간 변화가 안정적이다. insertion sort같은 것은 data가 어떻게 정렬되어 있는가에 따라 수행시간이 많이 달라지지만 mergesort는 한 Merge Step에서 데이터를 다 보기 때문에 알고리즘 면에서는 연산 수행시간 변화가 생길 요인이 없다.
3. Copy의 시간이 추가적으로 걸리는데, 따라서 데이터가 많은 경우에는 이런 Copy시간이 오래 걸릴 수 있다.
'알고리즘의 기초' 카테고리의 다른 글
| 1-(4) Divide and Conquer-(i) The maximum-subarray problem (0) | 2020.01.21 |
|---|---|
| 1-(3) Growth of Function (0) | 2020.01.20 |
| 1-(2) Getting Started-(i) Insertion Sort (0) | 2020.01.18 |
| 1-(1) The role of algorithms in computing (2) | 2020.01.17 |
| Introduction to algorithm (0) | 2020.01.17 |
- Total
- Today
- Yesterday
- 컴퓨터 과학
- Neural Network
- 자연어 처리
- gradient descent
- CS
- 컴퓨터과학
- 밑바닥부터 시작하는 딥러닝
- 머신 러닝
- 사진구조
- rnn
- 이산 신호
- NLP
- 이미지
- 영상구조
- 이미지처리
- 매트랩
- 신경망
- 신호 및 시스템
- Andrew ng
- 머신러닝
- 영상처리
- 매트랩 함수
- RGB이미지
- 순환 신경망
- ML
- 딥러닝
- Logistic Regression
- 인덱스 이미지
- 연속 신호
- CNN
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
