티스토리 뷰
문제

문제는 요약하면 다음과 같다. 8x8 체스판이 존재할 때 8개의 Queen을 서로 공격할 수 없는 위치에 배치하는 모든 경우의 수를 출력하라. 체스판 채우기 문제다. 완전탐색 문제라서 쉽다고 생각할 수 있지만, Search space를 줄이는게 관건인 테마인 만큼, 쓸데없는 search를 안 하기위해 신경써야한다.
※참고: Queen의 공격 범위는 십자와 대각선상 모든 점
Input: Test case의 개수 TC와 Queen을 반드시 배치해야 하는 (행,렬) 좌표
Output: 양식이 까다로우니 밑의 그림 참고
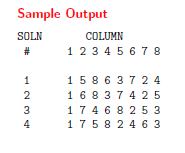
지금 완전탐색이라는 카테고리를 보고 있는데 이 문제는 그 중에서도 재귀적 퇴각 검색이라는 문제 카테고리에 속한다.
일단 코드부터 보자. 코드는 내가 다 짠 게 아니라 Halim, Steven, et al. Competitive Programming 3. Lulu Independent Publish, 2013.에서 가져와서 수정했음을 알린다. 알고리즘 보고 이해하는 것만 몇 시간 걸린 것 같다. Visual Studio는 좋은 디버거를 제공하니까 이해가 안 되는 알고리즘이 있으면 변수값을 확인해보며 디버깅하는게 이해하는데 도움이 될 수 있다.
이런 어려운 문제를 영어로 주석쓸 짬은 안돼서 좀 깨지지만 주석을 한글로 썼다.
#define _CRT_SECURE_NO_WARNINGS
#include<cstdio> //abs function()
#include<cstdlib>
#include<cstring>
int TC,row[8],a,b,lineCounter;
/*
row: Queen이 어디에 배치되었는가 저장하는 배열
row[c]: c열에 배치된 Queen의 행 좌표 저장.
TC: 입력받는 case의 수
lineCounter: solution의 수
*/
bool place(int r, int c) {
for (int prev = 0; prev < c; prev++) {//prev가 column
//모든 (row[prev],prev)에 대해 확인하는 절차
if (row[prev] == r || abs(row[prev] - r) == abs(prev - c)) {
return false; //같은 행에 있거나 같은 대각선 상에 있는 경우 배치 불가
/*
->왜 같은 열에 있는 Queen은 확인하지 않는가? : 같은 열에 있는 퀸을 확인하게 된다면, 재귀적 수행에서 같은 열에 배치된 지난 case를 보게 된다. 재귀적 수행이 불가하게됨.
->왜 모든 열에 대해 살펴보지 않는가? : 모든 열에 대해 살펴본다면 재귀적 수행이 불가능.
왜냐면 한 번 possible한 케이스가 정해진 후 다른 possible한 케이스를 구하는 과정에서 모든 열을 검사하게 된다면, 지난 case의 배치를 보게 된다.
*/
} //row[prev]:prev열에 배치된 Queen의 행좌표
//prev-c: column좌표 상 차이
}
return true;
}
void backtrack(int c) {
if (c == 8) { //후보 해
printf("%2d ", ++lineCounter);
for (int j = 0; j < 8; j++) {
printf(" %d", row[j] + 1);
}
printf("\n");
}
for (int r = 0; r < 8; r++) { //가능한 모든 해에 대한 시도
if (place(r, c)) { //만약 (r,c)자리에 Queen을 배치할 수 있다면
row[c] = r;
if (r == a && row[b] != a) break; //빠른 가지치기
backtrack(c + 1); // 이번 Queen을 여기에 배치하고 재귀를 수행한다.
}
}
}
int main() {
scanf("%d", &TC);
while (TC--) {
scanf("%d %d", &a, &b); --a; --b; //index가 0부터 시작하도록 변경한다.
memset(row, 0, sizeof(row)); //memset함수 -> memset(void* ptr, int value, size_t num);
lineCounter = 0; //solution의 개수 표시
printf("SOLN COLUMN\n");
printf(" # 1 2 3 4 5 6 7 8\n\n");
backtrack(0); //가능한 모든 8!개의 후보해를 생성한다.
if (TC) printf("\n"); //blank between each case
}
return 0;
}우선, 이 알고리즘은 column에 대한 재귀적 수행으로 작동된다. backtrack()함수가 재귀적 수행을 핵심적으로 담당하는 알고리즘이며 하나의 Chess판을 채우는 것은 row[0]~row[7]을 모두 채운 것과 동치로 여겨진다. 또한, 그렇게 다 채우게 된 경우(c==8로 terminal case에 돌입한 경우) 출력하는 part가 backtrack()에 존재한다.
backtrack(int c)함수는 채워야 할 c(column)가 주어진 경우 column 0~c-1까지 어떤 말들이 채워져 있다는 사실을 고려하여 해당 열 c에서 Queen을 배치할 수 있는 모든 행 r을 찾아서 Queen을 배치한 후 다음 열c+1로 넘어간다. 그런데 만약 해당 열 c에서 그런 r이 존재하지 않는다면 그 case는 불가능한 case이므로 아무것도 안해주면 된다. 그럼 0부터 c까지 재귀적으로 수행된 해당 case는 그냥 버려지게 된다.(그리고 그게 풀이에 맞다.) 이렇게 쭉쭉봐서 c==8까지 돌입하면 하나의 가능한 case가 완성된 것이므로 (a,b)에 말이 배치되어 있는 case인 경우인지(우리가 출력을 원하는 경우) 한번 더 검사를 해주고 출력해주면 된다.
또한, 이런 backtrack()함수에서 (r,c)에 말이 배치 가능한지 확인하는 함수가 bool place(int r,int c)인데 이 함수에서 주의해서 생각해야할 부분은 새로운 Queen의 (r,c)의 배치가능성을 검토할 때 다음 것은 검사하면 안된다.
- 해당 열 c에 Queen이 있는가?
- c+1~열에 있는 Queen들과의 충돌 가능성
이걸 검사한다면 하나의 case를 완성하게 된 후 다른 case를 출력하는게 불가능해진다.(Map은 하나의 가능한 case로 꽉 차 있을 것이므로)
따라서 0~c-1열에 대해서만 행과 대각선상 검사만 수행하면 된다. 코드가 어려우니까 여러번 생각해서 이해해보자. 그림을 그리면서 디버깅하는 것이 도움이 될 것 같다.
'기초 알고리즘 문제 풀이' 카테고리의 다른 글
| 32. Tips for exhaustive searching(Brute-force) (0) | 2020.02.27 |
|---|---|
| 31. Uva-927 Integer Sequences from Addition of Terms (0) | 2020.02.27 |
| 29. UVa-12455 Bars //Making subset using Bitmask-method (0) | 2020.02.25 |
| 28. UVa-725 Division //완전탐색, bitmask기법 (0) | 2020.02.24 |
| 27. UVa-10954 Add all //Greedy (0) | 2020.02.24 |
- Total
- Today
- Yesterday
- 신경망
- 매트랩 함수
- CNN
- 컴퓨터과학
- 딥러닝
- gradient descent
- rnn
- 매트랩
- NLP
- 컴퓨터 과학
- 이산 신호
- 영상구조
- 인덱스 이미지
- Neural Network
- 신호 및 시스템
- CS
- 밑바닥부터 시작하는 딥러닝
- 연속 신호
- 사진구조
- 머신 러닝
- 머신러닝
- ML
- 이미지
- Andrew ng
- 이미지처리
- 순환 신경망
- Logistic Regression
- 영상처리
- 자연어 처리
- RGB이미지
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
