티스토리 뷰
- 이 글은 하단의 Reference에 있는 강의, 교재를 보고 정리한 것입니다.
7.0 Intro
이번 장에서는 합성곱 신경망(Convolutional Neural Network)에 대해 다룬다. 이미지 인식에서 주로 사용되는 기법이다.
7.1 Overall Structure
합성곱 신경망은 기존의 신경망을 구성하는 Layer들에 추가로 Convolutional Layer, Pooling Layer를 추가로 이용해 만든다.
우선, 기존의 신경망은 인접하는 Layer간 모든 뉴런이 완전연결(Fully-Connected)되어있다는 특징이 있었고, 이 완전 연결된 계층을 Afiine 계층이라는 이름으로 구현했다. 이를 그림으로 표현해보면 다음<그림0>과 같다.
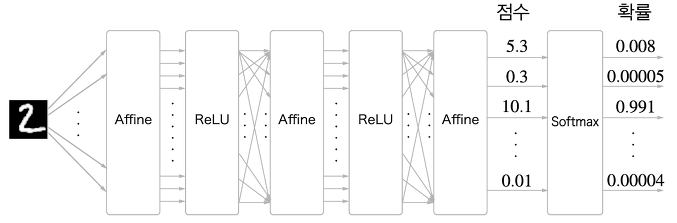
CNN은 다음 <그림1>과 같이 Conv layer, Pooling Layer를 추가하여 만들어지는 네트워크다.

Pooling 계층은 Conv,ReLU를 처리한 이후 들어가도 되고 안들어가도 된다. 또한 <그림1>과 같이 출력에 가까운 계층에서는 Fully connected layer를 사용할 수 있다.
7.2 Convolutional Layer
합성곱 계층의 구조와 계층의 연산에 대해 다룬다.
7.2.1 Problem of Fully connected layer
fully connected layer는 범용적으로 사용될 수 있는 가장 간단한 NN구조지만 다음과 같은 문제점을 갖고 있다.
-
데이터의 형상을 무시한다.
예를 들어 입력 데이터가 이미지인 경우 이미지는 가로x세로x채널 인 3차원으로, 이를 배치데이터로 만들면 4차원으로 구성되는데, 이것이 Fully connected layer에 처리할때는 1차원으로 펴져서 들어간다. 따라서 이미지의 공간적 특성이 모두 무시된다. 그러나 CNN은 input의 형상적 특성을 살려서 처리할 수 있으므로 이런 문제를 해결가능하다.
-
너무 많은 매개변수
Fully connected layer 구조를 생각해보면, 어떤 채널의 한 뉴런의 값은 이전 채널의 모든 뉴런 값에 의존한다. 즉,예를 들어 2층짜리 FC layer를 생각해보면, Data의 가로x세로x채널 을 평탄화 했을 때 값이 N이라 했을 때 이 2층짜리 FC layer에서 생기는 parmeter의 수는 N2개로 가로 28, 세로 28픽셀의 1채널(흑백) 이미지인 MNIST만을 생각해봐도, parameter는 (28x28)2개인 614,656 개가 나온다. 이렇게 parameter가 많으면 forward prop 의 계산양도 많을 것이고 메모리 소모도 클 수밖에 없다. CNN은 지역적 연결을 통해 output을 이전 layer의 some neurons와만 연결하여 이런 문제를 해결한다.
그래서 CNN의 특징을 다음과 같이 정리하기도 한다. 글을 먼저 읽고 나중에 돌아와서 한번 읽어보자.
- Local Connectivity(지역적 연결성): 특정 위치의 output은 모든 input에 의존하지 않고 some input에만 의존
- parameter sharing(매개변수 공유): 하나의 filter를 input에 돌려가며 적용하기 때문에 parameter를 적게 쓰며 공유
- pooling/subsampling hidden units
7.2.2 Convolution
합성곱 계층에서 하는 계산은 합성곱(Convolution)인데,여기서의 convolution은 수학적인 convolution과는 약간 차이가 있으므로 주의해야 한다. 합성곱 연산은 이미지 처리에서 말하는 필터 연산과 같은데, input에 filter를 동일 간격으로 이동해가며 합성곱을 계산한다. 이를 구체적인 예시를 통해 알아보자.
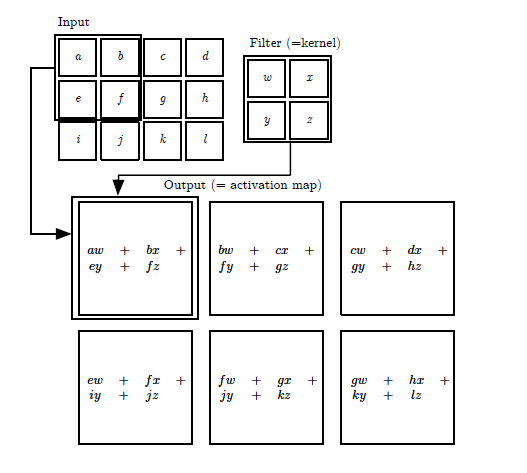
그림을 보면 input,kernel을 통해 output이 계산되고
- input: 3x4
- kernel: 2x2
- output:2x3
의 형상을 갖고있으며 output은 입력과 필터에서 각각 대응하는 원소끼리 곱한 후 그 총합을 계산하는 과정의 반복이다. 즉, 필터가 2x2이므로 input의 모든 가능한 2x2 영역에 2x2필터를 pointwise multiplication sum하는 것이다. 다음<그림3>의 GIF를 보면 노란색 필터 영역이 input을 돌아다니며 output을 계산하는 과정을 보여주고 있다.(필터의 값은 빨간색 글자다.)
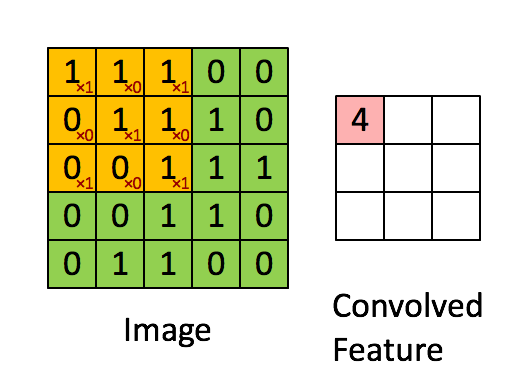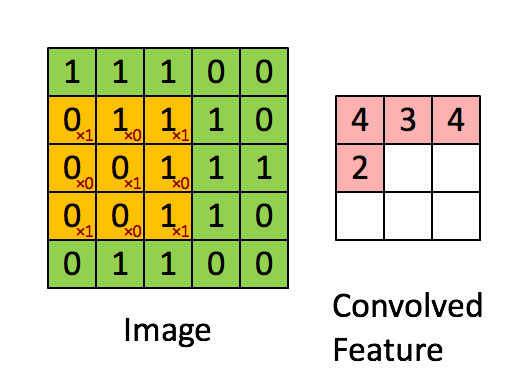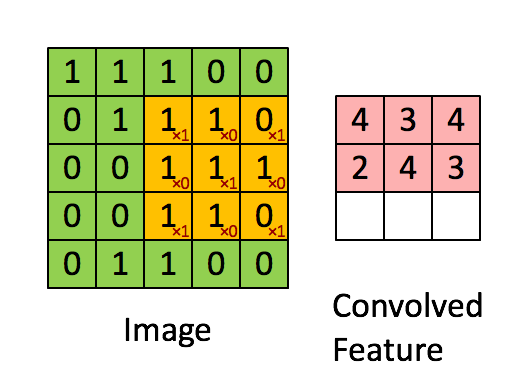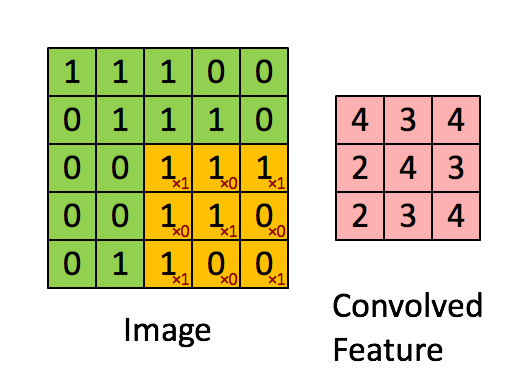
또한 합성곱 연산에서는 입출력 데이터를 Feature map이라고 부르기도 하는데 이런 Feature map이 위의 예제에서는 2차원이었다. 그러나 우리가 다루게 되는 일반적인 사진 데이터는 3차원이다. 그럼 이는 어떻게 처리하면 될까?
이전의 예시에서는 2차원 데이터를 2차원 필터로 처리했으므로, 3차원 데이터는 3차원 필터로 처리하면 된다. 다음의 <그림4>처럼 말이다.
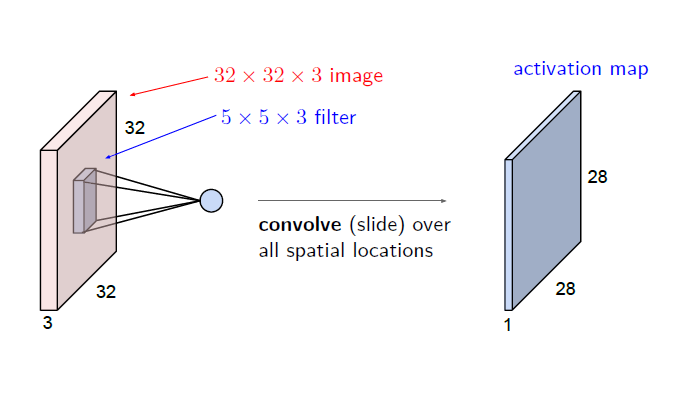
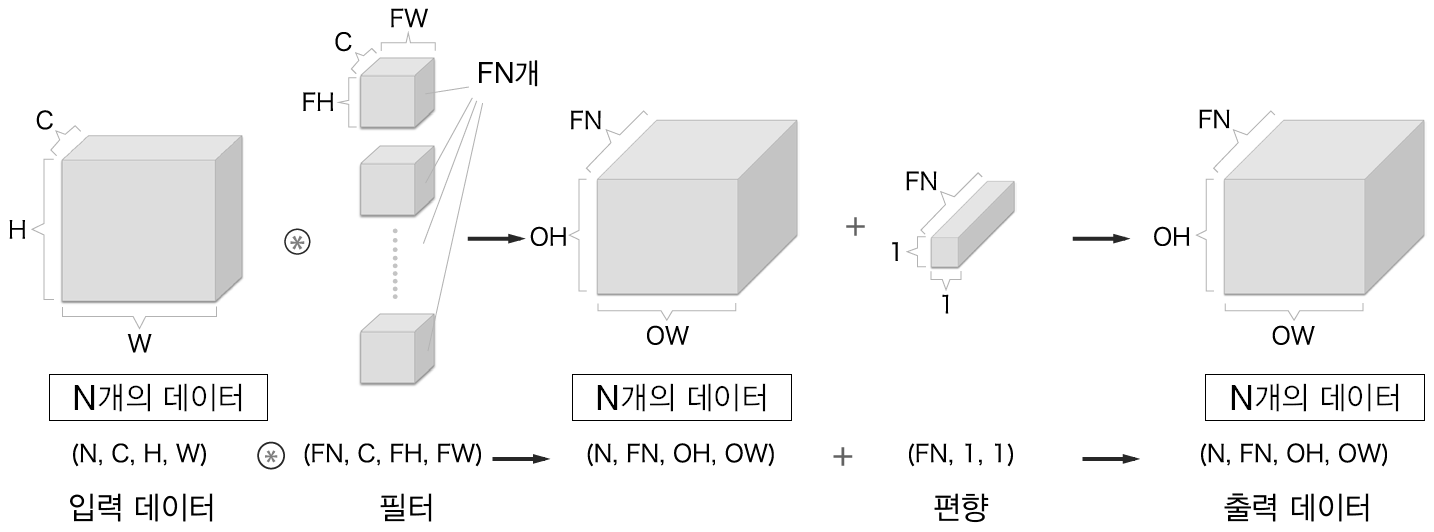
이 경우 input volume의 depth(3차원 길이)와 filetr의 depth가 같아야 함에 주의해야 한다. 또한, <그림4>에서 볼 수 있듯이 하나의 3차원 filter는 출력으로 하나의 activation map을 만들게 되는데, 이 activation map 하나의 차원은 2차원임에 주의해야 한다. 만약 output을 channel의 크기가 FN인 3차원으로 만들고 싶다면 이런 filter를 FN개 준비하면 된다. <그림5>는 이 내용을 모두 정리한 것이다. FN,C,FH,FW는 (출력 채널 수,입력 채널 수, 높이, 너비)를 뜻한다.
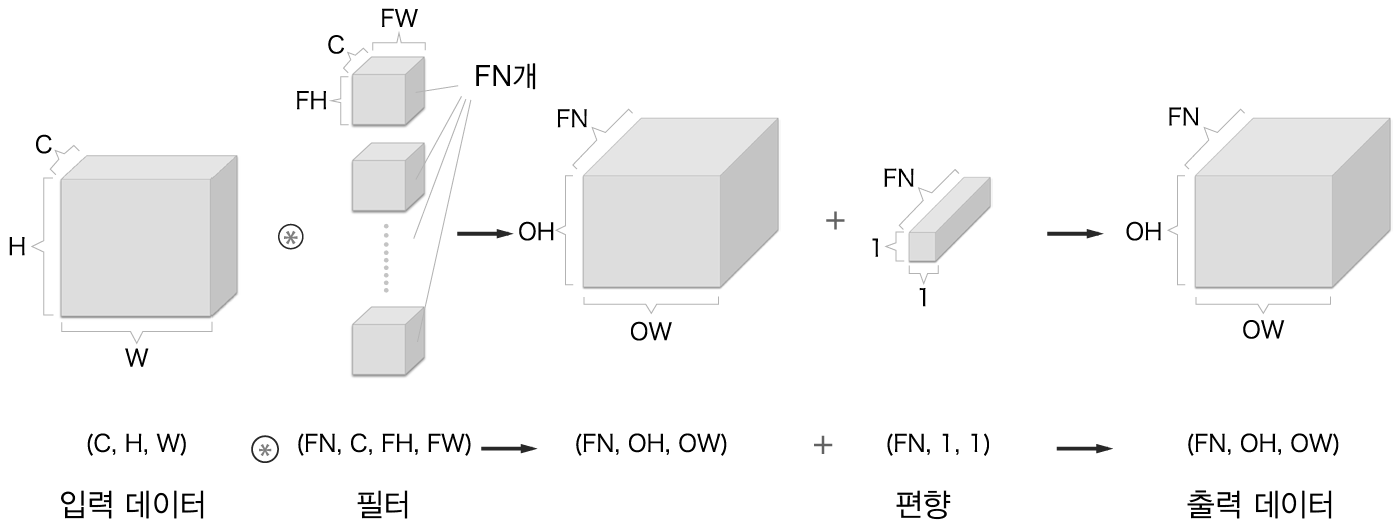
7.2.3 Batch processing
7.2.2까지는 하나의 데이터에 대한 합성곱 신경망의 처리였다. 그러나 데이터를 여러개 묶어 이를 배치 처리하게 되면 들어오는 데이터는 (데이터 수, 채널 수, 높이, 너비)의 4차원 형상을 갖게 되므로 데이터의 흐름은 다음 <그림6>과 같이 변한다.
7.2.4 Padding & Stride
합성 곱 연산은, 그 특성상 output의 크기가 input의 크기보다 작아질 수밖에 없다. 따라서 Convolution layer를 여러 층 쌓게되면 Feature map의 크기가 점점 작아지는 문제가 생기는데, 이런 상황에서 출력 크기를 조정할 목적으로 Padding을 사용한다.
Padding은 convolution 진행 시, input feature map 주변을 다음 <그림7>과 같이 0으로 채우는 방법이다. <그림7>에서는 4x4 크기의 입력 데이터에 폭 1짜리 패딩을 둘러 3x3필터에 합성곱을 진행한 모습이다.
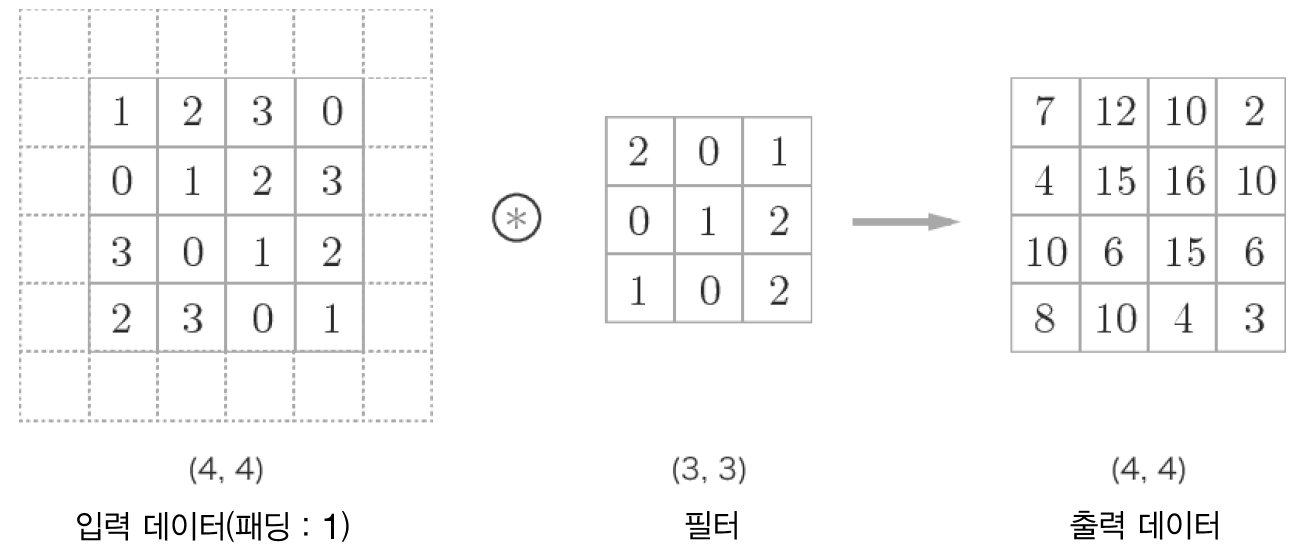
이 때 출력 데이터는 4x4크기가 되어 입력 데이터의 형상을 유지하는 것을 확인할 수 있다. 만약 출력의 크기를 키우고 싶다면 패딩의 폭을 더 늘리면 된다.
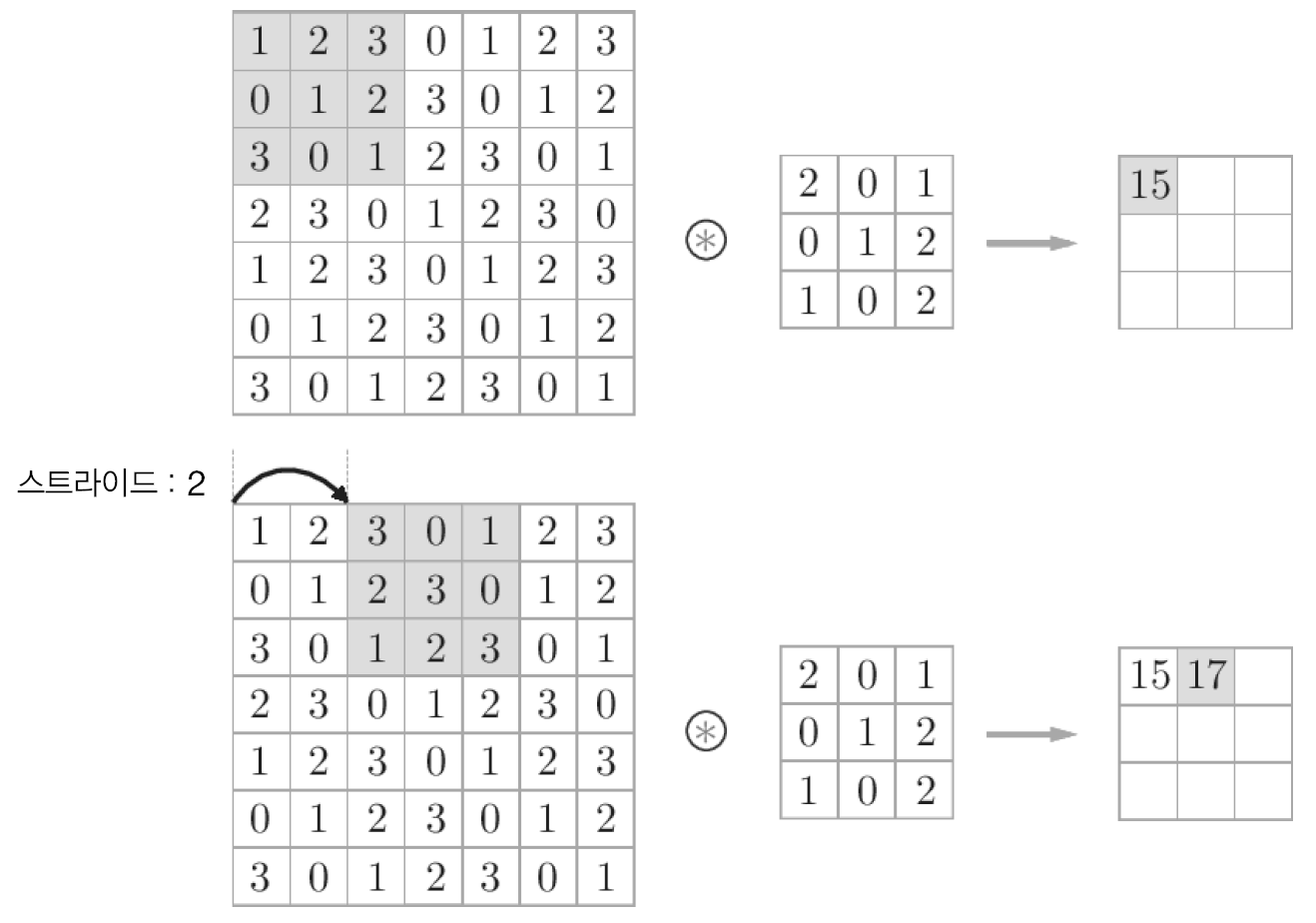
또한, 필터를 적용하는 간격을 Stride라 하는데 지금까지 본 예시는 모두 스트라이드가 1이었지만, 이를 임의의 크기로 설정할 수 있다. 예를 들어 스트라이드를 2로 하면 다음 <그림8>과 같이 계산 과정에서 필터는 두칸씩 이동한다.
7.2.5 Output size
이제 이 모두를 정리해서 입력 크기를 (H,W), 필터 크기를 (FH,FW), 출력 크기를 (OH,OW), 패딩을 P, 스트라이드를 S라 하면, 출력의 크기 OH,OW는 다음과 같이 계산된다. 이 값이 정수로 떨어지지 않으면 계산이 불가하게 만든 Framework들도 있으니 네트워크 구성 시 이 값이 정수가 되는지 확인할 필요가 있다.
$$
OH=\frac{H+2P-FH}{S}+1
$$
$$
OW = \frac{W+2P-FW}{S}+1
$$
7.3 Pooling Layer
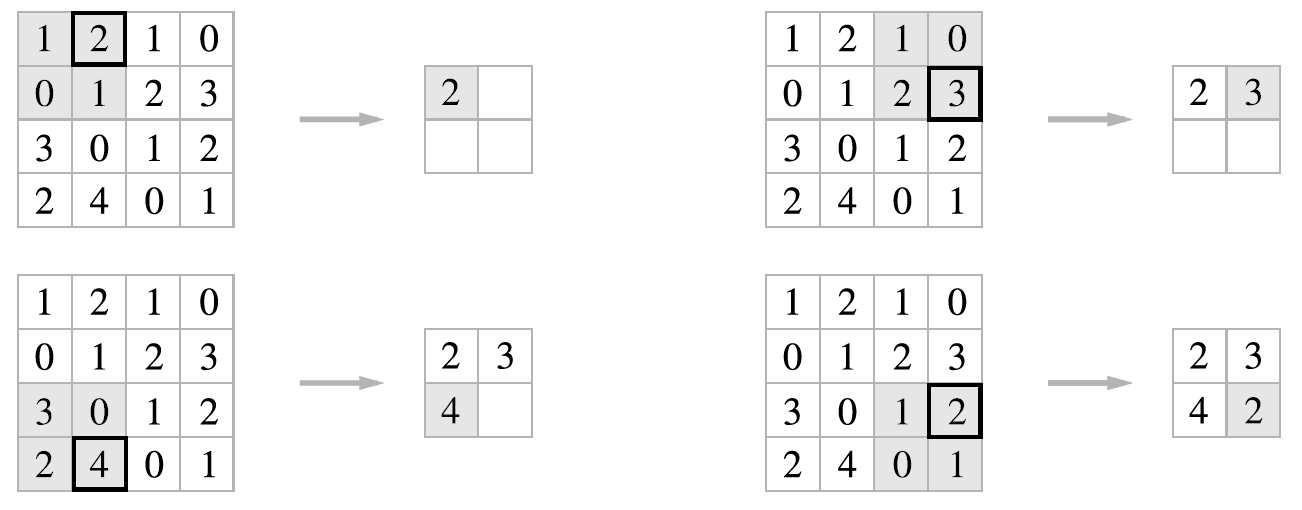
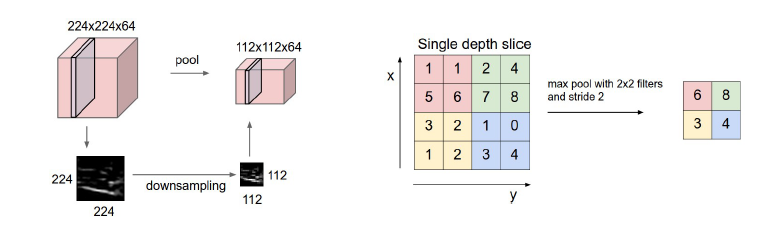
맨 처음 <그림1>에서 CNN에는 Conv layer외에도 Pooling layer가 있었다. 이 챕터에서는 Pooling Layer에 대해 다룬다. Pooling layer는 입력 feature map의 가로, 세로 방향 크기를 줄이는데 사용되는 기법으로 feature map의 정보를 downsampling하는 층이다. 정보를 요약하는 방법은 여러가지가 있지만, 다음 <그림9>는 max pooling 기법으로, 특정 영역 내의 max값만을 남기는 대표적인 pooling 방법이다. 2x2의 max pooling을 2의 stride로 적용하고 있다.
7.3.1 Feature of Pooling layer
Pooling layer는 다음과 같은 특징을 갖고 있다.
-
학습해야할 매개변수가 없다.
풀링 계층은 대상 영역에서 최대/평균등을 취하는 명확한 처리이므로 Convolutional Layer와 달리 특별히 학습해야할 매개변수가 없다.
-
input의 채널 수가 output에서 변하지 않는다.
채널마다 독립적으로 풀링 연산을 수행하기 때문에 입력 데이터의 채널 수 그대로 출력 데이터에 내보낸다. 다음 <그림10>을 보면 이해될 것이다.
-
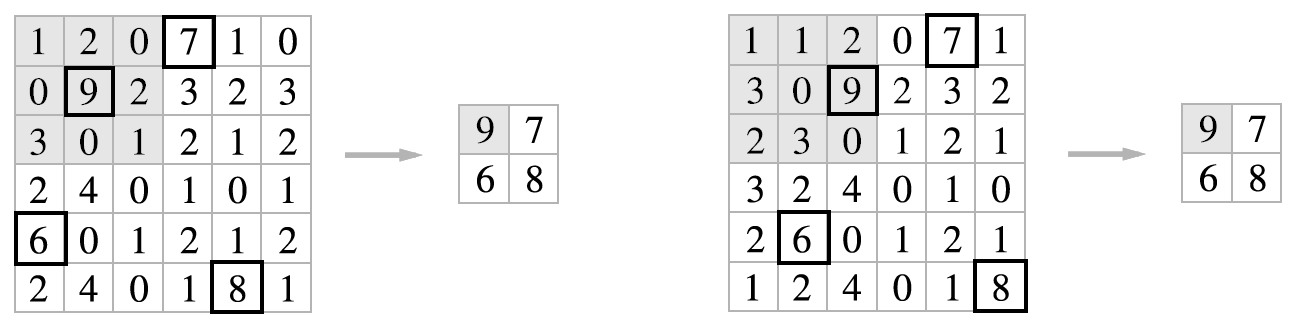
입력 데이터의 변화에 영향을 적게 받는다.
입력 데이터가 조금 변해도 풀링은 down sampling이므로 그 결과가 잘 변하지 않는다. 예를 들어 다음 <그림11>은 입력 데이터를 한 칸씩 오른쪽으로 이동시켰을 때 풀링 layer가 그 변화를 흡수한 상황을 나타낸다.
7.4 Implementing Layers
지금까지 다룬 Conv/Pooling layer들을 기본적인 라이브러리들만 이용하여 구현해본다. 코드의 출처는 밑의 Reference항목에 있다.
7.4.1 shape of input data
앞서 설명했듯이 batch처리시의 input data의 형상은 (N,C,H,W)로 4차원이다. 즉, 28x28의 흑백 사진 4개는 (4,1,28,28)로 처리된다. 따라서 각 개별 데이터에 접근하려면 x[0],x[1]과 같이 접근하면 된다. 또한, 이런 4차원 배열을 다음에 설명할 im2col이라는 함수를 통해 2차원으로 펼쳐 계산한다.
7.4.2 spreading data using im2col function
합성 곱 연산은 4차원이므로, 그대로 구현하려면 nested for loop을 사용해야 한다. 이는 성능이 떨어지므로 for문 대신 데이터의 형태를 바꾸어 계산을 진행한다.
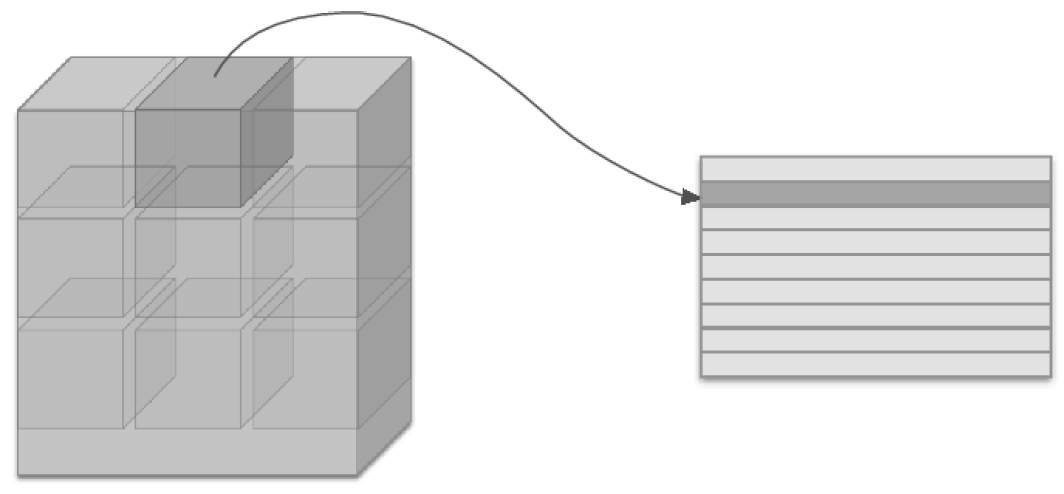
im2col은 입력 데이터를 필터링하기 좋게 전개하는 함수로 다음 <그림12>와 같이 하나의 데이터에서 각 필터링 적용 부분(3차원 블록)을 하나의 행(1차원)으로 펼치는 역활을 한다. 이렇게 되면 <그림12>의 결과에서 볼 수 있듯이 3차원인 데이터 한 개는 2차원 평면으로 펼쳐진다. batch처리시 그냥 이 작업을 모든 data에 반복하여 쭉 이어붙이면 된다.
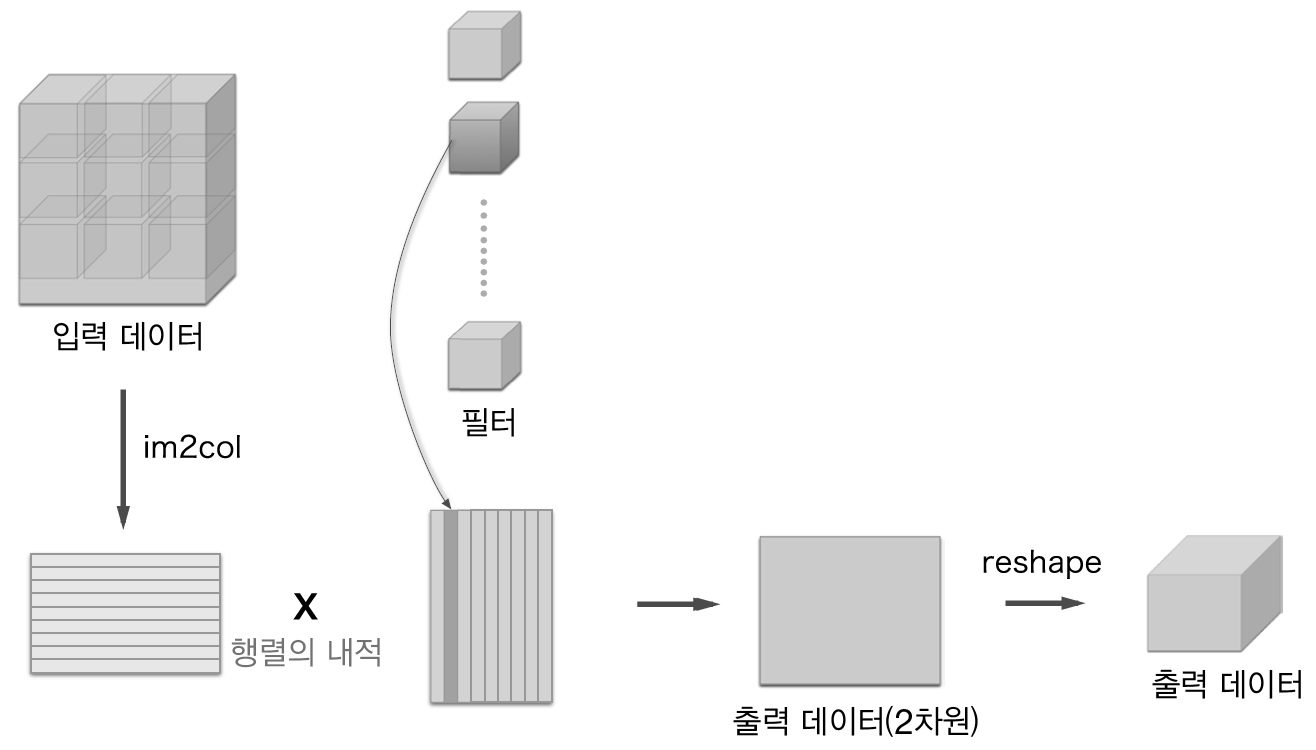
이후 <그림13>과 같이 하나의 필터를 하나의 열로 펼치게 되면 필터도 2차원 행렬로 나오게 되고 입력행렬의 행, 필터행렬의 열을 곱하는 행렬 연산이 곧 Convolution 연산이 된다. 이 연산의 결과물은 같은 2차원 행렬로 이를 다시 reshape하여 3차원으로 만든다. batch처리시 reshape의 결과물은 4차원이 된다.
이를 함수로 구현해보면 밑의 코드와 같다.
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
'''
다수의 이미지를 입력받아 2차원 배열로 변환한다(평탄화).
Parameters
----------
input_data : 4차원 배열 형태의 입력 데이터(이미지 수, 채널 수, 높이, 너비)
filter_h : 필터의 높이
filter_w : 필터의 너비
stride : 스트라이드
pad : 패딩
Returns
-------
col : 2차원 배열
'''
N, C, H, W = input_data.shape
# output의 크기 계산
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col7.4.3 Implemeniting Conv layer
해당 함수를 기반으로 convolution을 수행하는 layer를 구현해보면 다음 코드처럼 할 수 있다.
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 중간 데이터(backward 시 사용)
self.x = None
self.col = None
self.col_W = None
# 가중치와 편향 매개변수의 기울기
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape # 필터 수, 채널, 필터 높이, 필터 너비
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T # col과 행렬곱해야하므로 transpose하는게 맞음.
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2) # 형상을 (N,H,W,C) -> (N,C,H,W)로 바꾸어줌
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
# col2im->im2col의 역처리 함수
return dx7.4.4 Implementing Pooling Layer
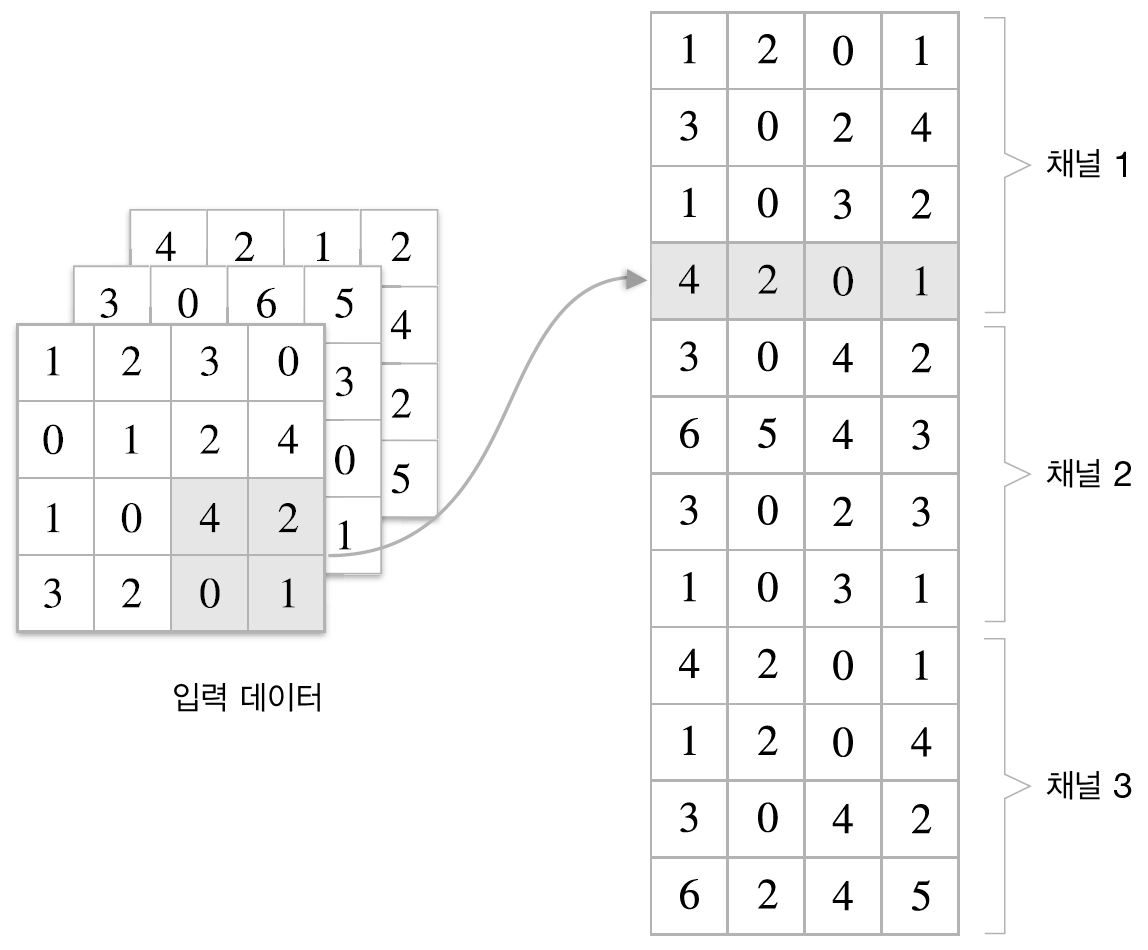
Pooling 계층도 im2col함수를 이용해 데이터를 전개하나 풀링 적용 영역은 각 채널별로 독립적이므로 다음 <그림14>와 같이 이를 채널별로 독립적으로 풀어내야한다. 이러면 각 영역이 하나의 행으로 펴지므로, 각 행별로 pooling 처리를 한 후, reshape하여 output data의 형상을 맞추어주면 된다.
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
# 0축의 max가 아니라 1축의 max
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max #어디서만 신호가 흘렀는지 기록해놓아야 함.(backward연산 위해)
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
참고로 axis= 1 일때 argmax,max의 출력결과는 다음 예시를 보고 이해하면 된다. axis=1일때 각 행별 최대를 출력함을 볼 수 있다.
x = np.array([[0,0,1,0],[1,0,0,0],[0,0,0,1],[0,1,0,0]])
print(np.argmax(x,axis=1))
>>[2 0 3 1]7.5 Implementing CNN
7.5.1 Constructing CNN
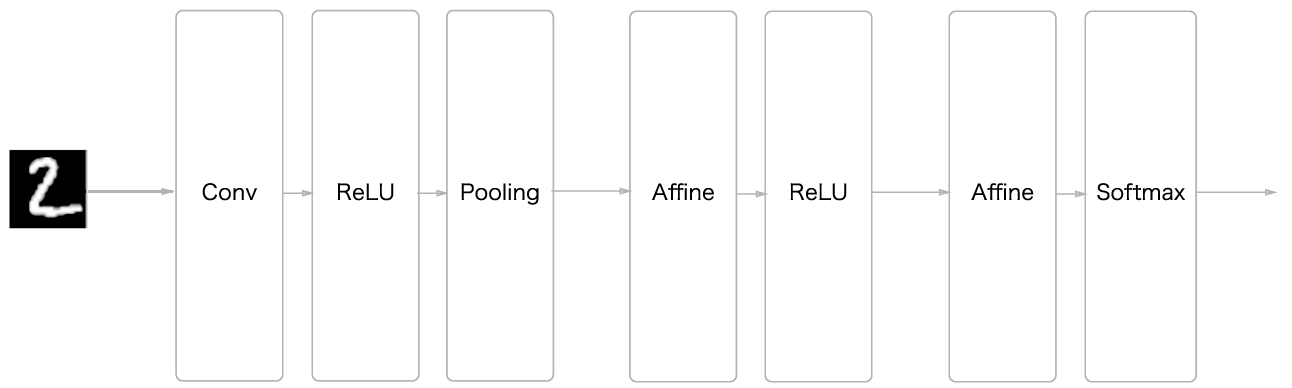
이미 구현된 layer 모듈들을 이용해 다음 <그림15>와 같은 simpleConvNet을 구성하여 MNIST set을 학습해보자.
from common.layers import *
class simpleConvNet:
def __init__(self,input_dim=(1,28,28),
conv_param={'filter_num':30,'filter_size':5,'pad':0,'stride':1},
hidden_size = 100, output_size = 10, weight_init_std=0.01):
# 1. 초기화 인수로 주어진 합성곱 계층의 parameter를 저장
# & output size 계산
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1] # 정사각형 데이터의 가정이 들어갔음.
conv_output_size = (input_size-filter_size+2*filter_pad)/filter_stride + 1
pool_output_size = int(filter_num*(conv_output_size/2)*(conv_output_size/2))
# 2. 가중치 매개변수의 초기화
self.params['W1'] = weight_init_std * np.random.randn(filter_num,input_dim[0],filter_size,filter_size) # 육면체의 filter를 생각. (FN,C,W,H)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size,hidden_size) # 육면체의 filter를 생각. (FN,C,W,H)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size,output_size)
self.params['b3'] = np.zeros(output_size)
# 3. Layer를 순서대로 쌓기
self.layers = orderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'],self.params['b1'],self.params['stride'],self.params['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2,pool_w=2,stride=2)
self.layers['Affine1'] = Affine(self.params['W2'],self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'],self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self,x):
#순전파
for layer in self.layers.value():
x = layer.forward(x)
return x
def loss(self,x,t):
return self.last_layer.forward(self.predict(x),t) # y=self.predict(x)
def gradient(self,x,t):
# 순전파
self.loss(x,t)
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
7.5.2 Training CNN
이 simpleNet을 이용하여 다음 코드로 MNIST dataset을 traning해보자.
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from common.trainer import Trainer
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 시간이 오래 걸릴 경우 데이터를 줄인다.
#x_train, t_train = x_train[:5000], t_train[:5000]
#x_test, t_test = x_test[:1000], t_test[:1000]
max_epochs = 20
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 매개변수 보존
network.save_params("params.pkl")
print("Saved Network Parameters!")
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
코드의 실행 결과는 다음 <그림16>과 같다. 이는 train data와 test data에 대한 accuracy를 plot해본 것이다.
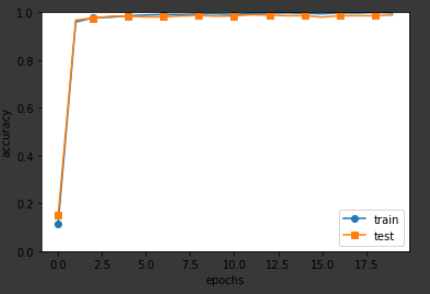
이 때 두 accuracy가 비슷하게 증가하는 경향을 보이고 있으며, 최종적으로 Test data에 대한 accuracy는 98.88%가 나와서 네트워크가 잘 학습된 것을 알 수 있다.
Reference
-그림2 출처: Goodfellow, Ian, et al. Deep learning. Vol. 1. Cambridge: MIT press, 2016.
-그림3,4,10 출처: Stanford CS231n Lecture
-그림0,1,5,6,7,8,9,11~ 16출처: Deep learning From scratch by Saito Goki
-All Codes by:https://github.com/WegraLee/deep-learning-from-scratch
'머신러닝' 카테고리의 다른 글
| [ML/NLP] 9. Simple Word2vec (0) | 2020.08.27 |
|---|---|
| [ML/NLP] 8. Distributional Representation of Words (0) | 2020.08.25 |
| [ML] 6. Back Propagation (2) | 2020.08.08 |
| [ML] 5. Training Neural Network (0) | 2020.08.06 |
| [ML] 4. Neural Network (0) | 2020.07.30 |
- Total
- Today
- Yesterday
- 컴퓨터 과학
- 사진구조
- RGB이미지
- CS
- gradient descent
- ML
- 머신러닝
- 컴퓨터과학
- 신경망
- 매트랩 함수
- 영상구조
- 딥러닝
- 밑바닥부터 시작하는 딥러닝
- 자연어 처리
- 이미지
- Logistic Regression
- rnn
- 머신 러닝
- 이산 신호
- 이미지처리
- 영상처리
- 순환 신경망
- CNN
- Neural Network
- NLP
- 매트랩
- 연속 신호
- Andrew ng
- 인덱스 이미지
- 신호 및 시스템
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
