티스토리 뷰
- 이 글은 하단의 Reference에 있는 강의, 교재를 보고 정리한 것입니다.
10.0 Intro
이 장에서는 word2vec을 개선하는 것을 목표로 한다. 이는 구체적으로 계산 병목이 발생하는 부분의 구조를 바꾸는 것으로
- embedding layer 도입
- negative sampling기법 사용
을 통해 수행된다.
10.1 Word2vec의 개선 방향
이전 장에서 다룬 Word2vec의 CBOW 모델은 맥락으로 2개의 단어를 사용할 때 다음 <그림1>과 같은 구조다.

이 구조는 어휘 수가 작은 corpus에 대해서는 별 문제없이 계산이 수행되나 어휘 수가 100만 정도 되는 corpus를 다룰 때는 다음 <그림2>와 같은 구조가 되고 계산 병목이 발생한다.

계산 병목이 발생하는 부분은 구체적으로 다음과 같다.
- 입력층으로부터 은닉층을 계산하는 행렬곱
- 은닉층으로부터 출력층(점수)를 계산하는 행렬곱
- 점수로부터 확률을 추출하는 Softmax 연산
첫번째로 입력인 one-hot vector로부터 은닉층의 값을 계산하는 부분은 Embedding 계층을 도입하는 것으로 개선할 수 있으며 두 번째 문제와 세번째 문제는 Negative sampling이라는 새로운 손실 함수를 도입함으로써 해결할 수 있다.
10.1.1 Embedding Layer
입력층으로부터 은닉층을 계산하는 행렬곱을 생각해보면, 어떤 1차원 벡터와 2차원인 행렬의 곱이고 이는 다음 <그림3>과 같이 수행된다.

그런데, 이 연산은 input의 특성을 생각해보면 매우 비효율적인 연산이다. 왜냐하면 input은 항상 하나의 값만이 1인 one-hot표현이기 때문에 이 벡터와 Win과의 행렬곱은 Win의 한 행벡터를 뽑아내는 연산이 되기 때문이다. 따라서 행렬곱 계층을 '단어 ID에 해당하는 행(벡터)'을 추출하는 계층으로 바꾼다면 이 계산 과정이 개선될 것이다. 이 계산을 수행하는 계층을 Embedding layer라 한다.
10.1.2 Implementing Embedding Layer
python상에서 2차원 numpy array의 k번째 행을 뽑아내는건 그냥 exarray[k]와 같이 수행하면 된다. k,l번째 행을 동시에 뽑아내려면 exarray[[k,l]]과 같이 수행할 수 있다. 따라서 embedding 계층의 forward연산은 다음과 같이 간단하게 구현될 수 있다.
# Embedding layer 1.
class Embedding:
def __init__(self,W):
self.params = [W] # W를 params list에 추가.
self.grads = [np.zeros_like(W)]
self.idx = None # backprop을 위해 필요한 attribute
def forward(self,idx): # idx: 통과하는 행
W, = self.params
self.idx = idx
out = W[idx]
return outparams는 이 책Deep Learning from scratch 2 by Saito Goki의 Trainer class 구현에 따라 W를 list에 넣은 것이고 grads도 마찬가지다. 참고로 W, = self.params 부분에서 왜 , 를 썼는지 의아할 수 있는데, 이는 W라는 list가 params라는 list안에 있는 list이기 때문이다. 그냥 다음 예제를 보고 콤마를 쓰고 안쓰고가 어떤 차이를 만드는지 확인해보자.
# EX1
import numpy as np
params = np.array([[1,2,4]])
W1, = params
print(W1)
W2 = params
print(W2)W1은 ,를 썻고 W2는 ,를 안 썼다. 둘 다 2차원 배열이다. 이 때 수행 결과는 다음과 같다.
# Result
[1 2 4]
[[1 2 4]]W2는 2차원 배열로 나와서 우리가 의도한 결과가 아님을 확인할 수 있다. 따라서 콤마연산을 함으로써 우리가 의도한 2차원이 1차원 배열로 풀리는 연산이 가능함을 확인할 수 있다.
이제 다시 layer구현으로 돌아와서 backward연산에 대해서 생각해보자. embedding layer의 순전파/역전파 연산을 그림으로 표현해보면 다음 <그림4>와 같다.

embedding layer에서 계층의 순전파는 특정 행을 추출하여 흘려보내는 것이었다. 따라서 역전파에서는 <그림4>에서처럼 앞 층(출력 쪽)으로부터 전해진 기울기를 다음 층(입력 쪽)으로 흘려보내기만 하면 된다.
# backward
def backward(self,dout):
dW, = self.grads
dW[...] = 0
for i,word_id in enumerate(self.idx):
dW[word_id] += dout[i]
# np.add.at(dW,self.idx,dout)
return None이 때 for문 부분은 왜 굳이 반복문으로 처리해야 하는지 이해가 안 될수도 있다. 그냥 dW[self.idx] = dout이렇게 하면 되는 것 아닌가? 그렇게 하면 다음 <그림5>와 같은 상황에 문제가 발생한다.

이런 경우 0번째 행에는 dh[0]만 반영되기 때문에 덧셈으로 둘 다 더해주어야 한다. for문 대신 np.add.at을 사용해 구현할 수도 있다. 이상으로 Embedding계층을 구현했다.
10.2 Word2vec의 개선방향2
앞서 언급한 문제 중
- 은닉층으로부터 출력층(점수)를 계산하는 행렬곱
- 점수로부터 확률을 추출하는 Softmax 연산
가 왜 문제가 되는지랑 이것을 해결하는 방법에 대해 다루어본다.
10.2.1 은닉층 이후 계산 병목
앞서 어휘가 100만개인 모델에서 계산 병목을 지적했는데, 어휘가 100만이면 출력층의 뉴런 수도 100만이기 때문에 출력층 쪽에서도 병목이 생길 수밖에 없다. 다음 <그림6>을 보자.

은닉층으로부터 출력층을 계산하는 부분은 행렬곱이므로 왜 계산 병목이 생기는지 이해할 수 있을 것이다. softmax는 바로 와닿지 않을 수 있지만 다음의 softmax 정의를 보면 분모의 값을 얻기 위해 exp계산이 100만번 필요하므로 계산 병목이 어휘 수에 비례하여 늘어나는 것을 알 수 있다.
$$
y_k=\frac{\exp(s_k)}{\sum _{ i=1}^{1000000}{\exp(s_i) } }
$$
10.2.2 다중 분류에서 이중 분류로
네거티브 샘플링기법에 대해 얘기한다. 이 기법은 다중분류를 이중분류로 근사하는 것이 핵심이므로 우선 그 주제에 대해 다룬다. 지금까지 word2vec에서 다뤄온 문제는 모두 '다중 분류'문제였다. 예를 들어 맥락으로 "you","goodbye"를 주면 여러가지 단어 중 "say"라는 단어를 출력할 확률을 높이는 모델을 만드는 것이 목표였다.
이제부터는 '다중 분류'문제를 '이중 분류'방식으로 해결하는 방법에 대해 생각해봐야하며, 그걸 위해서는 "Yes/No"로 답할 수 있는 질문을 생각해봐야 한다. 예컨대 "맥락이 You와 Goodbye일 때 타깃 단어는 say인가?"와 같은 문제는 예/아니오로 답할 수 있으므로 이중 분류 문제에 해당한다고 할 수 있다. 이런 이중 분류 문제는 신경망을 구성할 때 다음 <그림7>과 같이 출력층에 뉴런이 하나만 필요하다.

이렇게 출력층의 뉴런이 하나로 변하면 은닉층에서 출력층을 계산하는 행렬곱은 Wout의 "say"에 해당하는 열벡터와 은닉층의 내적 계산이 된다. 이 계산을 자세히 나타내보면 다음 <그림8>과 같다.
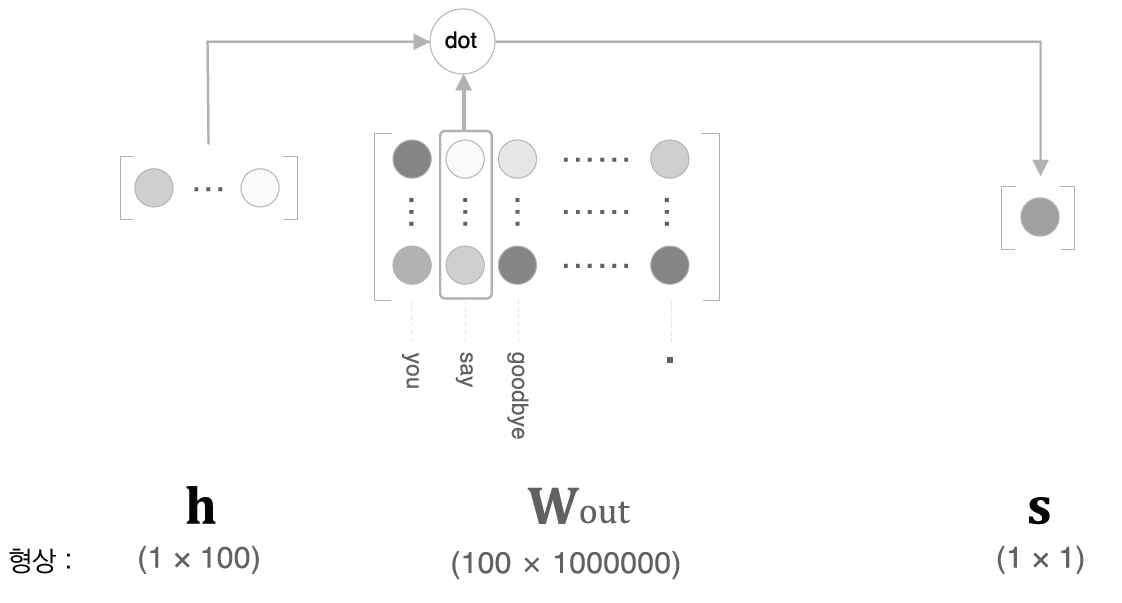
이런 이중 분류를 모든 단어에 대해 수행할 수 있게 된다면, 이는 곧 다중 분류를 수행할 수 있게 됨을 의미한다.
10.2.3 시그모이드 함수와 엔트로피 오차
이진 분류 문제를 신경망으로 풀기 위해서는
- 점수에 sigmoid 함수를 적용해 확률로 변환
- 손실을 구할 때 손실 함수로 cross-entropy error 사용
하는 과정을 흔히 사용한다. sigmoid와 cross-entropy error 계층에 대해서는 이전 포스트들에서 설명했으므로 간략하게 설명하겠다.
sigmoid는 다음과 같이 정의되는 함수다.
$$
y= \frac{1}{1+\exp(-x)}
$$
이를 layer로 다음 <그림9>과 같이 구현한다.

이렇게 얻어낸 확률값 y에 대해 cross entropy Loss는 다음과 같이 계산된다.
$$
L = -(t\log{y}+(1-t)\log{(1-y)})
$$
이 두 과정을 합쳐 다음 <그림10>과 같이 sigmoid-with-loss layer를 구현할 수 있다. 또한 cross entropy 계층과 sigmoid계층을 지난 역전파 값은 결국 깔끔하게 y-t로 계산된다.
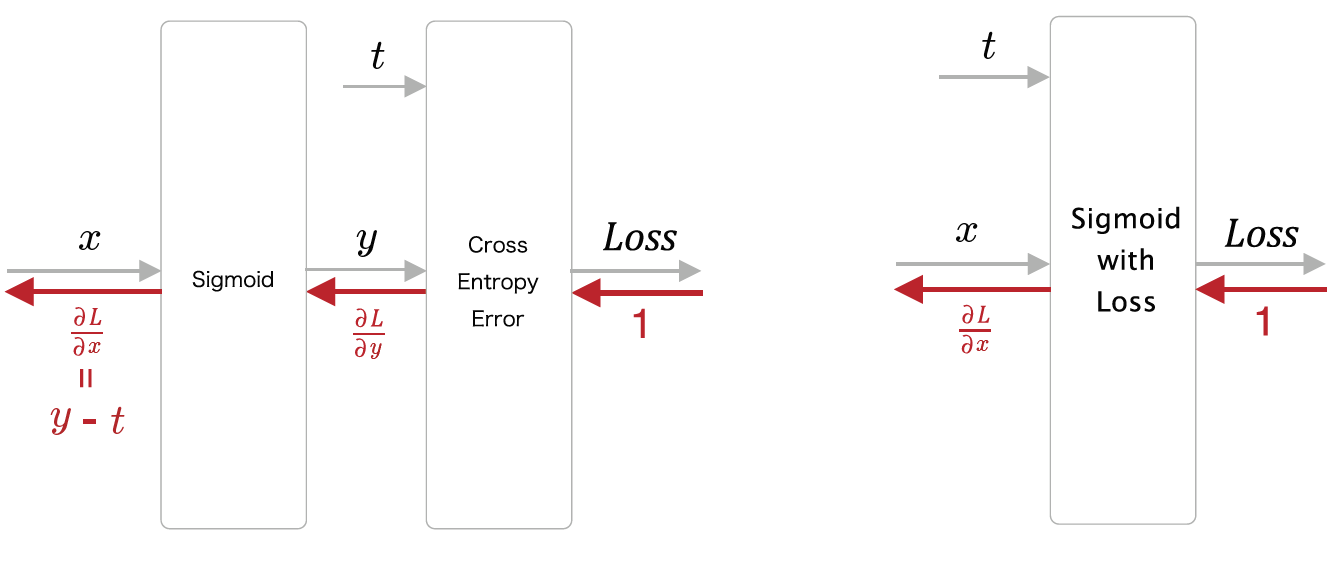
10.2.4 다중 분류에서 이진 분류 구현하기
앞서 얘기한 모든 과정들을 쭉 layer들의 흐름으로 합쳐보면 다음 <그림11>과 같다.

<그림11>의 구성에서 h는 은닉층 벡터이며 이 값과 Wout의 열 하나를 내적하면 점수가 나오기 때 문에 Wout의 열 하나를 내보내는 Embed계층을 h와 dot로 연결한다. 이렇게 출력된 점수를 정답 레이블(1/0)과 함께 Sigmoid with loss 계층에 넣으면 Loss가 출력된다. 이제 h 이후의 구조를 조금 더 보기좋게 만들기 위해 Embed와 dot를 동시에 수행해주는 EmbeddingDot layer를 구현하자.
# EmbeddingDot layer
class EmbeddingDot:
def __init__(self,W):
self.embed = Embedding(W)
self.params = self.embed.params # dot기능은 parameter가 필요없음
self.grads = self.embed.grads
self.cache = None
def forward(self,h,idx): # idx 는 array가 될 수 있음(미니배치 가정)
target_W = self.embed.forward(idx)
out = np.sum(target_W*h,axis=1) # out은 array가 될 수 있기 때문에 단순히 np.sum은 X
self.cache = (h,target_W)
return out
def backward(self,dout):
h,target_W = self.cache
dout = dout.reshape(dout.shape[0],1) # 1행 n열벡터를 n행 1열 벡터로 변경
dtarget_W = dout*h
dh = dout*target_W
return dh
10.2.5 네거티브 샘플링
생각해보면 지금까지 다룬 것들은 모두 긍정적 예시에 대한 것들이었다. 예를 들어 "I"와 "goodbye"사이에 "say"가 올 때 Loss와 신경망의 출력을 구해서 학습시키는 것이었다. 그러나 다중 분류 문제를 이중 분류 문제로 다루려면 정답과 오답에 대해 각각 바르게 분류할 수 있어야 하므로, 나머지 어휘들을 대상으로 하는 추론에 대해서도 신경망은 이진 분류를 할 수 있어야 한다. 즉, 긍정적 예시("say")에 대해서는 Sigmoid 계층의 출력을 1에, 부정적 예시("say"외의 단어)에 대해서는 sigmoid 계층의 출력을 0에 가깝게 만들어야 한다.
이 때 모든 부정적 예시를 대상으로 이진 분류를 학습시킨다면 어휘 수가 많아짐에 따라 학습이 너무 힘들어지므로, 근사적인 해법으로 적은 수의 부정적인 예를 몇 개 선택해서(샘플링해서) 사용한다. 이것을 네거티브 샘플링 기법이라 한다. 구체적으로 방법을 설명하면
- 긍정적 예를 타깃으로 한 경우의 손실을 구한다.
- 부정적 예를 몇 개 샘플링하여 그것에 대해서도 마찬가지로 손실을 구한다.
- 각각의 데아터에 대한 손실을 더한 값을 최종 손실로 계산
마지막 순서에서 Loss를 더하면 각 예시에 대한 grads갱신이 제대로 되지 않는 것이 아닌가 생각할 수 있지만, <그림12>의 구조를 보면 Backprop에서 각 예제에 대해 grads 갱신은 모든 Embedding dot layer별로 이루어지는 구조이므로 괜찮다. 그리고 어차피 벡터 표현은 Win것을 사용하면되므로 <그림12>에 있는 여러개의 Wout중 어떤 것을 벡터 표현으로 쓸 지 고민하지 않아도 된다.
10.2.6 샘플링 기법
네거티브 샘플링에서 어떤 샘플을 뽑을지에 대해서도 생각해봐야 한다. 처음에는 그냥 부정적 예시 중 랜덤으로 뽑으면 되지 않을까 생각해볼 수 있지만 효과적인 샘플링 기법이 존재한다. 이는 말뭉치 통계 데이터를 기초로 샘플링 하는 방법으로, 말뭉치에서 자주 등장하는 단어를 많이 추출하고 드물게 등장하는 단어를 적게 추출하는 방법이다. 이 때 각 단어의 등장 확률 P(wi)에 대해 이것을 그냥 활용하는 것보다는 다음과 같이 0.75를 제곱한 값을 사용하는 것이 더욱 효과적이라고 알려져있다. 이 수정된 식은 원래 확률이 낮은 단어의 확률을 살짝 높여주는 역할을 한다. 확률 간 대소관계는 유지된다. (분모는 확률의 합을 1로 맞춰주기 위한 조치다.)
$$
P'(w_i)=\frac{P(w_i)^{0.75}}{\sum _{j=1 }^{ n }{ P(w_j) } }
$$
이 책 Deep Learning from scratch 2 by Saito Goki에서는 제공된 UnigramSampler클래스를 사용한다.
10.2.7 네거티브 샘플링 구현
class NegativeSamplingLoss:
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads = [], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
def forward(self, h, target):
batch_size = target.shape[0]
negative_sample = self.sampler.get_negative_sample(target) # sample 뽑음
# 긍정적 예 순전파 - 하나
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# 부정적 예 순전파 - 여러개에 대해
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample_size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label) # Loss는 총합
return loss
def backward(self, dout=1):
dh = 0
# 병렬연결되어있는 각 계층(embeddot->loss)마다 이를 역순으로 backward prop해주기
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = l0.backward(dout) # loss가 뒷쪽에 연결되어있으므로 loss부터 backprop해야함.
dh += l1.backward(dscore) # 총 dh는 다 더한거.
return dh
참고로 backward에서 dh가 모든 dh의 합인 이유는 원래 h가 순전파 될 때는 복사되었기 때문이다. (Repeat node역할)
10.3 개선된 Word2vec 구현과 학습
10.3.1 CBOW 구현
지금까지 개선한 것들을 바탕으로 제대로 된 CBOW 모델을 구현해보자.
import sys
sys.path.append('..')
import numpy as np
from common.layers import *
from ch04.negative_sampling_layer import NegativeSamplingLoss
class CBOW:
def __init__(self,vocab_size,hidden_size,window_size,corpus):
V,H = vocab_size,hidden_size
# 가중치 초기화
W_in = 0.01 * np.random.randn(V,H).astype('f')
W_out = 0.01 * np.random.randn(V,H).astype('f') # input과 동일 형상 맞음
# 계층
self.in_layers = []
for i in range(2*window_size):
layer = Embedding(W_in) # input쪽에 Embedding layer는 맥락의 수만큼 필요함.
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out,corpus,power=0.75,sample_size=5)
# 모든 가중치 & 기울기를 배열에 모아야함(training method규정)
layers = self.in_layers + [self.ns_loss]
self.params,self.grads = [],[]
for layer in layers:
self.params += layer.params
self.grads += layer.grads
self.word_vecs = W_in # word_vec 표현 저장
# 파이썬은 객체복사이므로 W_in이 변하면 word_vecs도 변함!
def forward(self,contexts,target):
h=0
for i,layer in enumerate(self.in_layers):
h += layer.forward(contexts[:,i])
h *= 1/len(self.in_layers) # h는 여러 layer 출력의 평균으로 정함
loss = self.ns_loss.forward(h,target)
return loss
def backward(self,dout=1):
dout = self.ns_loss.backward(dout) # 제일 뒤에 있는 계층부터
dout *= 1/len(self.in_layers)
for layer in self.in_layers: # 병렬 연결이므로 이들 간 backward 순서는 상관 X
layer.backward(dout)
return None
10.3.2 모델 훈련
Training은 다음과 같이 하자.
# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
from common import config
# GPU에서 실행하려면 아래 주석을 해제하세요(CuPy 필요).
# ===============================================
# config.GPU = True
# ===============================================
import pickle
from common.trainer import Trainer
from common.optimizer import Adam
from cbow import CBOW
from skip_gram import SkipGram
from common.util import create_contexts_target, to_cpu, to_gpu
from dataset import ptb
# 하이퍼파라미터 설정
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10
# 데이터 읽기
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
contexts, target = to_gpu(contexts), to_gpu(target)
# 모델 등 생성
model = CBOW(vocab_size, hidden_size, window_size, corpus)
# model = SkipGram(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)
# 학습 시작
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
# 나중에 사용할 수 있도록 필요한 데이터 저장
word_vecs = model.word_vecs
if config.GPU:
word_vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl' # or 'skipgram_params.pkl'
with open(pkl_file, 'wb') as f:
pickle.dump(params, f, -1)
10.3.3 모델 평가
most_similar함수를 이용해서 가장 비슷한 query를 5개씩 뽑아보자.
import sys
sys.path.append('..')
from common.util import *
import pickle
pkl_file = 'cbow_params.pkl'
with open(pkl_file,'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
querys = ['you','year','car','toyota']
for query in querys:
most_similar(query,word_to_id,id_to_word,word_vecs,top=5)실행 결과는 다음 결과와 같았다. top similar단어들은 꽤 성공적으로 출력된것을 확인할 수 있다.
[query] you
we: 0.6103515625
someone: 0.59130859375
i: 0.55419921875
something: 0.48974609375
anyone: 0.47314453125
[query] year
month: 0.71875
week: 0.65234375
spring: 0.62744140625
summer: 0.6259765625
decade: 0.603515625
[query] car
luxury: 0.497314453125
arabia: 0.47802734375
auto: 0.47119140625
disk-drive: 0.450927734375
travel: 0.4091796875
[query] toyota
ford: 0.55078125
instrumentation: 0.509765625
mazda: 0.49365234375
bethlehem: 0.47509765625
nissan: 0.474853515625또한, word2vec은 이런 유사 단어 찾기 외에 유추 문제를 풀기에도 적합한 점으로 유리한데 예를들어 king:queen = man:?와 같은 문제를 생각해볼 수 있다. 이 때 ?에 기대하는 단어는 woman으로 이 작업을 수행해주는 함수인 analogy()함수가 책에 구현되어 있으므로 사용해보면 유추 작업에 대해 몇가지 결과를 얻을 수 있다.
다음과 같이 코드를 작성해보자.
analogy('king','man','queen',word_to_id,id_to_word,word_vecs)
analogy('take','took','go',word_to_id,id_to_word,word_vecs)그럼 결과가 다음과 같이 유추 작업을 잘 수행해내는 것을 확인할 수 있다. 물론 안되는 경우도 많다.
[analogy] king:man = queen:?
woman: 5.16015625
veto: 4.9296875
ounce: 4.69140625
earthquake: 4.6328125
successor: 4.609375
[analogy] take:took = go:?
went: 4.55078125
points: 4.25
began: 4.09375
comes: 3.98046875
oct.: 3.90625Reference
All pictures on: Deep Learning from scratch 2 by Saito Goki
All codes on: https://github.com/WegraLee/deep-learning-from-scratch-2
'머신러닝' 카테고리의 다른 글
| [ML/NLP] 11. RNN (0) | 2020.09.10 |
|---|---|
| [ML/NLP] 9. Simple Word2vec (0) | 2020.08.27 |
| [ML/NLP] 8. Distributional Representation of Words (0) | 2020.08.25 |
| [ML] 7. Convolutional Neural Network (0) | 2020.08.22 |
| [ML] 6. Back Propagation (2) | 2020.08.08 |
- Total
- Today
- Yesterday
- 연속 신호
- rnn
- 영상구조
- CNN
- Neural Network
- 영상처리
- 순환 신경망
- 이미지처리
- 사진구조
- RGB이미지
- Logistic Regression
- ML
- 신호 및 시스템
- 인덱스 이미지
- 머신 러닝
- CS
- 매트랩 함수
- 신경망
- 컴퓨터과학
- 이미지
- NLP
- 밑바닥부터 시작하는 딥러닝
- 머신러닝
- 이산 신호
- 컴퓨터 과학
- 매트랩
- 딥러닝
- Andrew ng
- gradient descent
- 자연어 처리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
