티스토리 뷰
- 이 글은 하단의 Reference에 있는 강의, 교재를 보고 정리한 것입니다.
11.0 Intro
지금까지 다룬 Fully connected layer, word2vec, CNN 등은 항상 신호가 단방향으로 흐르는 피드포워드라는 유형의 신경망이었다. 이런 유형의 신경망은 그 구조가 단순하여 이해하기 쉽다는 장점이 있다. 그러나 시계열 데이터를 잘 다루지 못한다는 단점이 있다. 더 정확히는 단순한 피드포워드 신경망에서는 시계열 데이터의 성질(패턴)을 충분히 학습할 수 없다. 그래서 순환 신경망Recurrent Neural Network(RNN)을 도입하게 된다. 이번 장에서는
- 언어 모델의 확률적 관점에서의 기술
- RNN구조
- RNN구현
- RNNLM
- RNNLM의 구현과 평가
에 대해 다룬다.
11.1 Probability & Language Model
이번 절에서는 RNN을 다루기 위해 먼저 앞 장의 word2vec을 확률적 관점에서 기술하고 이를 바탕으로 언어를 확률로 다루는 언어 모델에 대해 설명한다. 11.1.1은 아래 글의 9.5를 요약한 것이므로 본문을 읽고 와도 좋다.
word2vec의 확률적 관점: https://hezma.tistory.com/103
11.1.1 Probablistic aspect of word2vec
CBOW 모델을 확률적 관점에서 기술해보자. 쓰이는 수학적 기술법은 아래에 있는 것 정도만 알면 된다.
- P(A): A라는 사건이 발생할 확률
- P(A|B): B가 일어났을 때, A가 일어날 확률 (사후 확률, 조건부 확률)
- P(A,B): A와 B가 동시에 발생할 확률
CBOW 모델이 하는 일은 맥락이 주어졌을 때, 타깃이 출현할 확률을 계산하는 것이다. 여기서는 <그림1>처럼 T개의 단어로 이루어진 말뭉치를 w1,w2,...,wT의 단어 시퀀스로 표기하고, t번째 단어 wt에 대해 윈도우 크기가 1인 맥락을 고려해보자.

이 때 맥락으로 wt-1과wt+1이 주어졌을 때 wt가 출현할 확률은, 두 단어의 동시 발생시 타깃이 일어날 확률이므로
$$
P(w_t|w_{t-1},w_{t+1})
$$
과 같이 표기할 수 있다. 즉, CBOW 모델은 상기 식을 모델링 하고 있는 것이다.
이 식을 이용하면 CBOW 모델의 손실 함수도 간결하게 표현할 수 있다. cross-entropy-error를 적용한 손실 함수는 다음 식과 같이 정의된다.
$$
L=-\sum_{k}{t_k\log{y_k}}
$$
(tk:정답 레이블, yk: 모델의 출력, 각 레이블은 one-hot encoding 되어있었음)
즉, 정답 레이블에 해당하는 모델의 출력만을 log에 넣어 부호반전 시킨것의 합이 Loss였으므로 그대로 CBOW 모델의 것을 적용해보면,
- 정답 레이블은 'wt가 발생'이므로 wt에 해당하는 원소만 1
- 이 것에 해당하는 모델의 출력은 'wt가 발생할 확률'이므로 P(w|..)과 같은 꼴
따라서 CBOW에서 하나의 단어 wt에 해당하는 loss는 다음 식과 같이 정의된다. 이런 식의 형태를 음의 로그 가능도라 부른다.
$$
L = -\log{P(w_t|w_{t-1},w_{t+1})}
$$
이를 말뭉치 전체에 대하여 확장하면, 다음과 같다.
$$
L = -\frac{1}{T}\sum{\log{P(w_t|w_{t-1},w_{t+1})}}
$$
따라서 CBOW model의 학습은 이 손실함수의 값을 작게 만드는 것이 되고, 이것을 달성하는 가중치 W가 단어의 분산 표현이 될 것이다.
이처럼 CBOW 모델을 학습시키는 본래 목적은 맥락으로부터 타깃을 정확하게 추측하는 것이고, 그 부산물로 단어의 의미가 인코딩된 단어의 분산 표현을 얻을 수 있다. 그럼 CBOW모델의 본래 목적인 '맥락으로부터 타깃을 추측하는 작업'은 어디에 이용할 수 있을까? 위의 식 P(wt|wt-2,wt-1)은 실용적인 쓰임이 있을까? 이 두 질문에 대답하기 위해 언어 모델이 등장한다.
11.1.2 Language Model
언어 모델Language Model은 단어 나열에 확률을 부여한다. 즉, 그 시퀀스가 일어날 확률이 어느 정도일지 확률로 평가하는 것이다. 예를 들어 "You say goodbye"와 같이 자연스러운 단어의 나열에 대해서는 높은 확률을 출력하고 "You say good die"와 같이 부자연스러운 단어의 나열에는 낮은 확률을 출력하는 것이다. 이 언어 모델은 기계 번역과 음성 인식등에 다양하게 응용되고 새로운 문장을 생성하는 데도 응용될 수 있다.
언어 모델을 수학적으로 이해하기 위해 w1,w2,w3....,wm-1,wm으로 이루어진 문장(단어 시퀀스)을 생각해보자. 이 때 단어가 그 순서로 출현할 확률을 언어 모델에서는 P(w1,....,wm)로 나타낸다. 이 동시 확률은 사후 확률과 곱셈정리를 사용하여 다음과 같이 사후 확률들의 곱으로 분해해 쓸 수 있다.

즉 최종 사후 확률은 각 타깃 단어에서 타깃 단어보다 왼쪽에 있는 모든 단어를 맥락으로 했을 때의 사후 확률의 곱이 된다. 이를 그림으로 표현해보면 다음 <그림2>와 같다.

즉, 우리의 목표는 P(wt|w1,...,wt-1)을 얻는 것이다. 이 확률을 계산할 수 있다면 언어 모델의 동시 확률 P(w1,....,wm)을 얻을 수 있기 때문이다.
11.1.3 Representing CBOW as Language Model
그렇다면 CBOW 모델을 언어 모델에 적용하려면 어떻게 해야할까? 이는 맥락의 크기를 특정 값으로 한정하여 근사적으로 나타낼 수 있다. 다음 식은 맥락을 왼쪽 2개의 단어로 한정했을 때의 표현이다.

이 모델에서 맥락의 크기는 임의로 설정할 수 있다. 그러나 결국 맥락은 특정 길이로 고정해야하므로 CBOW 모델을 만들면 맥락보다 더 왼쪽에 있는 단어는 무시된다. 예를 들어 왼쪽 10개의 단어를 맥락으로 CBOW모델을 만들면 그 맥락보다 더 왼쪽에 있는 단어는 무시된다. 이것은 긴 맥락이 필요한 추론에서 문제가 되는데, 다음<그림3>이 그런 예시다.

이 경우 ?에 답하려면 Tom을 기억해야 한다. 따라서 맥락의 크기가 10이라면 이 문제에 제대로 답할 수 없다. 그렇다고 맥락을 키우기만 하면 문제가 해결될까? 물론 CBOW 모델에서 맥락의 크기는 임의로 설정할 수 있으나, CBOW모델에서는 맥락 안의 단어 순서가 무시된다는 한계가 존재한다. 왜냐하면 계산시 다음 <그림4>의 왼쪽과 같이 단어 벡터가 더해져서 평균값이 은닉층에 오기 때문이다. 즉 (you,say)와 (say,you)를 같은 맥락 취급할 것이다.

그래서 신경 확률론적 언어 모델Neural Probablistic Language Model에서는 <그림4>의 오른쪽 모델처럼 맥락의 단어 순서를 고려한 모델을 제안한다. 하지만 이 모델은 맥락의 크기에 비례해 가중치 매개변수가 늘어나는 한계가 있다. 따라서 이 문제를 해결하기 위해 RNN이 제안된다.
11.2 RNN
RNNRecurrent Neural Network을 직역하면 순환하는 신경망으로 그 구조가 신호를 순환시키기 때문에 붙은 이름이다. 이번 절에서는 RNN의 구조와 신호 흐름에 대해 알아본다.
11.2.1 Structure of RNN
RNN은 다음 <그림5>와 같은 RNN 계층이 모여져 만들어지는 구조다.

이 <그림5>처럼 RNN 계층은 순환하는 경로를 포함한다. 이 순환 경로를 통해 데이터를 계층 안에서 순환시킬 수 있다. 또한 <그림5>에서는 xt를 입력 받는데 이는 시계열 데이터 (x0,...,xt,...)가 RNN계층에 입력됨을 표현한 것이다. 그리고 그 입력에 대응하여 (h0,...ht,..)가 출력된다. 또한 각 시각에 입력되는 xt는 벡터인데, 예를 들어 문장에서는 xt가 각 단어의 분산표현이 될 것이며, 이 분산 표현이 순서대로 하나씩 RNN계층에 입력되는 것이다.
이 RNN에서 신호의 흐름은 RNN을 다음 <그림6>과 같이 펼쳐진 신경망으로 그리면 이해하기 쉬워진다. 오른쪽의 펼쳐진 구조는 우리가 항상 봐오던 피드포워드 신경망과 비슷한 꼴이기 때문이다. 펼쳐진 RNN 계층들이 실제로는 모두 같은 RNN계층이라는 것이 피드 포워드 신경망과의 차이점이다.

<그림6>을 보면 알 수 있듯, 각 시각의 RNN계층은 이전 시각의 출력과 현 시각의 입력을 받아 이로부터 현 시각의 출력을 계산한다. 구체적으로는 다음과 같은 식에 의해 계산된다.
$$
h_t = \tanh{(h_{t-1}W_h+x_tW_x+b)}
$$
이 식에는 두 개의 가중치가 있으며 Wh는 이전 시각의 출력에 대한 가중치, Wx는 현재 입력에 대한 가중치다. 또한 편향 b도 존재한다. 이 신호들의 합이 쌍곡 탄젠트 함수 tanh에 변환되어 그 결과과 시각 t의 출력 ht가 된다. 이 ht는 (RNN과는)다른 계층을 향해 위쪽으로 출력되는 동시에 다음 시각의 RNN계층(자기 자신)을 향해 오른쪽으로도 출력된다.여기서 ht는 자기 자신에게 전달되기 때문에 RNN을 신호가 순환하는 계층으로 설명한다.
그리고 식을 보면 현재 상태의 출력은 이전 상태의 출력에 기초하여 계산된다. 이를 다른 과점에서 보면 RNN은 h라는 상태를 가지고 있으며 상기 식의 형태로 상태를 갱신한다고 해석할 수 있다. 그래서 RNN계층을 상태를 가지는 계층, 메모리가 있는 계층등으로 부르기도 하며 h를 은닉 상태hidden state 혹은 은닉 상태 벡터hidden state vector로 부르기도 한다.
또한 현재 다루고 있는 책 Deep Learning from scratch 2 by Saito Goki에서는 <그림7>의 오른쪽과 같이 RNN을 나타내고 있으나 많은 문헌에서는 <그림7>의 왼쪽과 같은 방식으로 나타내기도 한다.

11.2.2 BPTT
앞에서 보았듯 RNN 계층은 가로로 펼친 신경망으로 표현할 수 있다. 따라서 RNN 계층의 학습도 다음 <그림8>과 같이 일반적인 신경망과 같은 순서로 진행할 수 있다.

<그림8>에서 볼 수 있듯이 순환 구조를 펼친 후의 RNN은 일반적인 오차역전파법을 적용할 수 있다. 여기서의 오차역전파법은 '시간 방향으로 펼친 신경망의 오차역전파법'이라는 뜻으로 BPTTBackpropagation Through Time라 한다. 이 BPTT를 이용하면 RNN을 학습할 수 있지만 이런 방식의 오차역전파법에는 문제가 하나 있다. 그것은 바로 긴 시계열 데이터를 학습할 때 매 시각 RNN 계층의 중간 데이터를 메모리에 유지해야하기 때문에 컴퓨팅 자원과 메모리의 소모가 커진다는 것이다. 또한 시간 크기가 커지면 역전파 시의 기울기가 불안정해지는 것도 문제가 된다.
11.2.3 Truncated BPTT
위의 문제를 해결하기 위해 큰 시계열 데이터를 취급할 때는 역전파의 연결을 적당한 길이마다 끊는다. 즉, 시간축 방향으로 너무 길어진 신경망을 적당한 지점에서 잘라내 작은 신경망 여러개로 만들고, 각각의 작은 신경망에서 오차역전파법을 수행하는 것으로 이것이 바로 Truncated BPTT라는 기법이다. 이 때 조심해야 할 것은 끊는 것은 역전파 뿐으로, 순전파는 끊지 않는다는 것이다.
예를 들어 길이가 1000인 시계열 데이터를 다루는 것을 생각해보자. 이 경우 RNN을 펼쳐보면 1000개의 RNN 계층이 존재할 것이다. 이렇게 계층의 길이가 너무 길어지면 기울기 계산시 계산량과 메모리 사용량이 문제가 되고, 신경망을 하나 통과할 때마다 기울기 값이 조금씩 작아져서 이전 시각 t까지 역전파되기 전에 0이 되어 소멸할 가능성도 있다. 그래서 Truncated BPTT에서는 RNN의 역전파를 다음 <그림9>와 같이 중간중간에서 끊는다. <그림9>는 10개씩 끊은 예시다.

<그림9>처럼 역전파를 끊어버리면 그보다 미래의 데이터에 대해서는 생각할 필요가 없다. 따라서 각각의 회색 블록은 미래의 블록과는 독립적으로 오차역전파법을 연결시킬 수 있다. 이제 Truncated BPTT에서 차근차근 순전파와 역전파하는 과정을 알아보자. <그림9>에서 우선 첫번째 블록의 순전파와 역전파를 다음<그림10>과 같이 수행한다. 한 블록 내에서 순전파를 완성하면 굳이 모든 시계열 데이터를 볼 필요 없이 역전파를 진행할 수 있으므로, 블록 내에서는 순전파 후 바로 역전파를 진행할 수 있다.

이제 다음 블록에서의 순전파는 이전 블록 마지막 RNN계층의 은닉 상태 벡터를 받아서 진행한다. 역전파는 마찬가지로 블록 내에서 독립적으로 수행된다. 세번째 블록부터는 두번째 블록과 마찬가지이므로 모든 과정을 다음 <그림11>과 같이 정리할 수 있다.

11.2.4 Minibatch Learning of Truncated BPTT
이전까지의 서술은 전부 미니배치=1로 하나의 시계열 데이터만을 보는 경우를 생각했으므로 여러 데이터를 한 번에 처리하는 경우에 대해서도 생각해봐야한다. 예를 들어 x0,...,x999으로 이루어진 시계열 데이터를 2개의 미니배치로 구성하여 학습하는 경우를 생각해보자. 역전파가 이루어지는 각 블록은 10개의 RNN layer로 이루어져있다.
이 경우 첫번째 미니배치는 원래대로 처음 위치인 x0에서 시작하여 x0~x9로 이루어진 블록에 대해서 진행한다. 두 번째 미니배치는 1000/2=500으로 x500에서 시작하여 x500~x509로 이루어진 블록에 대해서 진행하면 된다. 즉 동시에 진행하는 시작점이 두개인 것처럼 진행하면 된다. <그림12>는 이 과정을 그림으로 나타낸 것이다. 또한 하나의 미니배치가 끝에 도달하면 다시 처음에 시작한 지점부터 데이터를 입력하도록 하면 된다.

이 과정이 배치 수가 늘어나고 데이터가 배치수로 딱 떨어지지 않는 경우에는 미니배치가 끝에 도달한 경우의 처리가 조금 헷갈리게 되는데, 이는 코드로 구현 후 디버깅을 해보면서 이해해보는 편이 빠르다. 밑의 구현 과정에서 어떻게 이 미니배치가 이뤄지는지 디버깅 과정을 다루어놓았다.
11.3 Implementing RNN
이제 실제로 RNN을 구현해보자. 구체적으로는 Truncated BPTT를 따르는 미니배치 RNN이 된다. 또한 우리가 다루는 신경망은 길이가 T인 시계열 데이터를 받아 각 시각의 은닉 상태를 T개 출력하는 모델인데, 이를 하나의 모듈로 다음 <그림13>과 같이 구현해본다.

이 구조와 같이 입력과 출력을 하나로 묶으면, 모듈에서의 입력은 길이 T의 xs, 출력은 길이 T인 hs가 된다.. 이 묶은 모듈을 Deep Learning from scratch 2 by Saito Goki에서는 T개분의 작업을 한 번에 처리하는 Time RNN 계층이라 한다.
11.3.1 Implementing RNN layer
RNN처리를 한 단계만 수행하는 RNN클래스부터 구현해보자. 우선 순전파는 다음 식을 구현하면 된다.
$$
h_t = \tanh{(h_{t-1}W_h+x_tW_x+b)}
$$
우리는 N개의 데이터를 미니배치로 모아 처리하므로 xt와 ht에는 각 샘플 데이터가 행방향으로 저장되어있다. 따라서 계산시 각 데이터와 가중치의 형상은 다음 <그림14>와 같다.
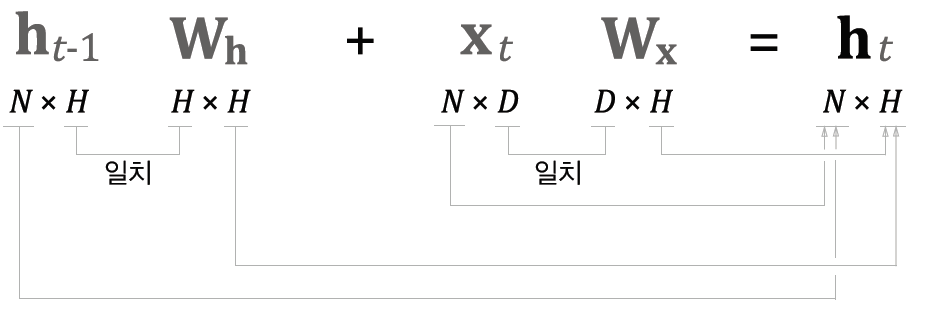
여기까지의 순전파를 코드로 구현해보면 다음과 같다.
# Implementing RNN layer
class RNN:
def __init__(self,Wx,Wh,b):
self.params = [Wx,Wh,b] # parameter초기화
self.grads = [np.zeros_like(Wx),np.zeros_like(Wh),np.zeros_like(b)] # gradients의 초기화
self.cache = None # backprop을 위한 cache
def forward(self,x,h_prev):
Wx,Wh,b = self.params
t = np.matmul(h_prev,Wh)+np.matmul(x,Wx)+b
h_next = np.tanh(h)
self.cache = (x,h_prev,h_next)
return h_next이제는 RNN의 역전파를 구현해야하는데, 이를 위해 RNN 계층의 순전파 계산 그래프를 다음 <그림15>와 같이 MatMul, +, tanh를 이용하여 표현할 수 있다.

이렇게 되면 총 갱신해야 하는 매개변수는 세 종류-Wx,Wh,b쪽으로 기울기를 전파해야하고, 나머지 input signal인 hprev와 x방향으로도 기울기를 전파해야 한다. 계산 노드의 역전파법칙을 이용해 역전파 계산을 해보면 다음과 같이 코드를 작성할 수 있다.
# Implementing Backward
def backward(self,dh_next):
Wx,Wh,b = self.params
x,h_prev,h_next = self.cache
dt = dh_next * (1-h_next**2)
db = np.sum(dt,axis=0)
dWh = np.matmul(h_prev.T,dt)
dh_prev = np.matmul(dt,Wh.T)
dWx = np.matmul(x.T,dt)
dx = np.matmul(dt,Wx.T)
self.grads[0][...]=dWx
self.grads[1][...]=dWh
self.grads[2][...]=db
return dx,dh_prev이제는 이 기본 RNN을 이용하여 T개의 기본 RNN이 묶인 Time RNN계층을 구현해보자.
11.3.2 Implementing Time RNN layer
우선 코드부터 보자
# 초기화
class TimeRNN:
def __init__(self,Wx,Wh,b,stateful=False):
# Stateful: 이전 은닉 상태를 인가받을 것인가?->forward 계산시 이전 은닉 상태가 필요하므로
self.params = [Wx,Wh,b]
self.grads = [np.zeros_like(Wx),np.zeros_like(Wh),np.zeros_like(b)]
self.layers = None # 다수의 RNN 계층을 리스트로 저장하는 용도
self.h, self.dh = None,None
self.stateful = stateful
def set_state(self,h):
self.h = h
def reset_state(self):
self.h = None초기화 메서드는 그 내용을 이해하기 쉬울 것이다. set_state와 reset_state는 은닉상태를 변경하는 메서드로, 확장성을 고려하여 집어넣었으며 stateful변수는 이전 은닉상태를 인가받을지 결정하는 변수다. stateful 분기에 관심을 갖고 다음의 forward 구현을 보자.
# 순전파
def forward(self,xs): # xs->T개 분량의 시계열 데이터
Wx,Wh,b = self.params
N,T,D = xs.shape
D,H = Wx.shape
self.layers = []
hs = np.empty((N,T,H),dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N,H),dtype='f')
for t in range(T):
layer = RNN(*self.params)
self.h = layer.forward(xs[:,t,:],self.h)
hs[:,t,:]=self.h
self.layers.append(layer)
return hs순전파는 T의 길이를 가진 시계열 데이터 N개를 xs라는 변수로 받아서 총 T번 RNN을 순차적으로 호출하며 연쇄적인 개별 forward 계산을 수행한다. 이 때 for문 앞의 if문은 stateful 변수가 false거나 h가 None일 때 h를 영행렬로 채워주는 역할을 한다. h가 None인 경우는 맨 처음 순전파를 수행할 때이다. 만약 두번째 블록에서 forward가 수행되면 이전의 h가 남아있을 것이므로 h는 None이 아니다.
이제 역전파를 구현해보자. 이 역전파의 계산 그래프는 다음 <그림16>과 같다.

<그림16>에서는 TimeRNN의 상위 계층에서 전해지는 기울기를 dhs라 했고 하류로 내보내는 기울기를 dxs라 했다. Truncated BPTT를 구현하고 있으므로 이후 layer의 역전파는 필요하지 않다. 단 그 시각의 기울기는 확장성을 위해 dh에 저장해놓는다. 또한 TimeRNN내부에서는 다음 <그림17>과 같이 역전파가 일어난다.

하나의 RNN에는 상위 흐름에서 받은 dht와 미래 RNN계층에서의 dhnext가 더해져서 입력되고 하위 계층과 이전 시각 RNN계층으로 각각 dxt와dhprev가 입력된다. TimeRNN의 총 입력과 총 출력은 dhs,dxs이므로 이에 주의하여 역전파 코드를 작성해보면 다음과 같다.
# 역전파
def backward(self,dhs):
Wx,Wh,b = self.params
N,T,H = dhs.shape
D,H = Wx,shape
dxs = np.empty((N,T,D),dtype='f')
dh=0
grads = [0,0,0]
for t in reversed(range(T)):
layer = self.layers[t]
dx,dh = layer.backward(dhs[:,t,:]+dh) # dh에는 미래 시각의 것이 저장되어있음
dxs[:,t,:]=dx
for i,grad in enumerate(layer.grads):
grads[i] += grad
for i,grad in enumerate(grads):
self.grads[i][...]= grad
self.dh = dh
return dxs사전 준비는 크게 어렵지 않게 할 수 있다. 중요한 것은 T번 반복되는 for문으로 순전파시 저장했던 layer들에 대해 역순으로 backward를 호출하고 있다.
이로써 TimeRNN계층의 구현이 끝났다.
11.4 RNN Language Model
이번장의 목표는 RNN을 사용하여 언어 모델 구현하기다. 이는 Time RNN에 몇가지 시계열 데이터 처리 계층을 붙인것으로 RNNLM이라 칭하기도 한다.
11.4.1 Structure of RNNLM
RNNLM에서 사용되는 신경망의 구조는 다음 <그림18>과 같다. 각 신경망에 들어오는 벡터의 크기도 표시했으며 배치처리를 고려하지 않은 형상이다. 빨간색 네모 칸 안의 형상은 가중치의 형상이다.

<그림18>의 첫번째 층은 Embedding계층으로 단어 ID를 입력받아 단어의 분산 표현으로 바꾸어준다. 이 단어의 분산 표현은 이전 시각의 hidden state vector와 함께 RNN계층으로 입력되고, RNN은 hiddens state vector를 출력한다. 이 hidden state는 다음 시각의 RNN계층과 위쪽 Affine계층->SoftMaxwithLoss계층으로 전달되어 최종적으로 특정 시각에서 Vx1크기의 확률 분포 벡터를 출력한다. 이 확률 분포 벡터는 각 단어가 출현할 확률을 나타내는 것으로 생각할 수 있다. 예를 들어 샘플 말뭉치로 "You say goodbye and I say hello."라는 문장이 주어졌을 때 RNNLM에서는 다음 <그림19>와 같은 입/출력이 존재한다. 단어 ID는 Vx1의 one-hot encoded vector다.

이 때 정보 흐름을 보면 goodbye자리에서 다음에 올 단어를 추측하는데는 you,say,goodbye의 hidden vector만이 사용되었으므로 RNNLM은 현재까지 나온 단어들을 기반으로 다음에 오는 단어를 추측하는 신경망인 것을 알 수 있다. 다른 시각으로 보면 RNN은 "you say"라는 과거의 정보를 응집된 hidden state vector로 기억하고 있으며 이를 더 위의 Affine계층, 다음 시각의 RNN계층에 전달하는 것이 RNNLM에서 RNN의 역할이라 볼 수 있다.
11.4.2 Time layers in RNNLM
RNNLM을 구성할 때 <그림19>에 있는 것처럼 모든 계층을 다 따로 구현하지말고 다음 <그림20>처럼 Time 계층으로 묶어 구현하는 방법을 생각해볼 수 있다.
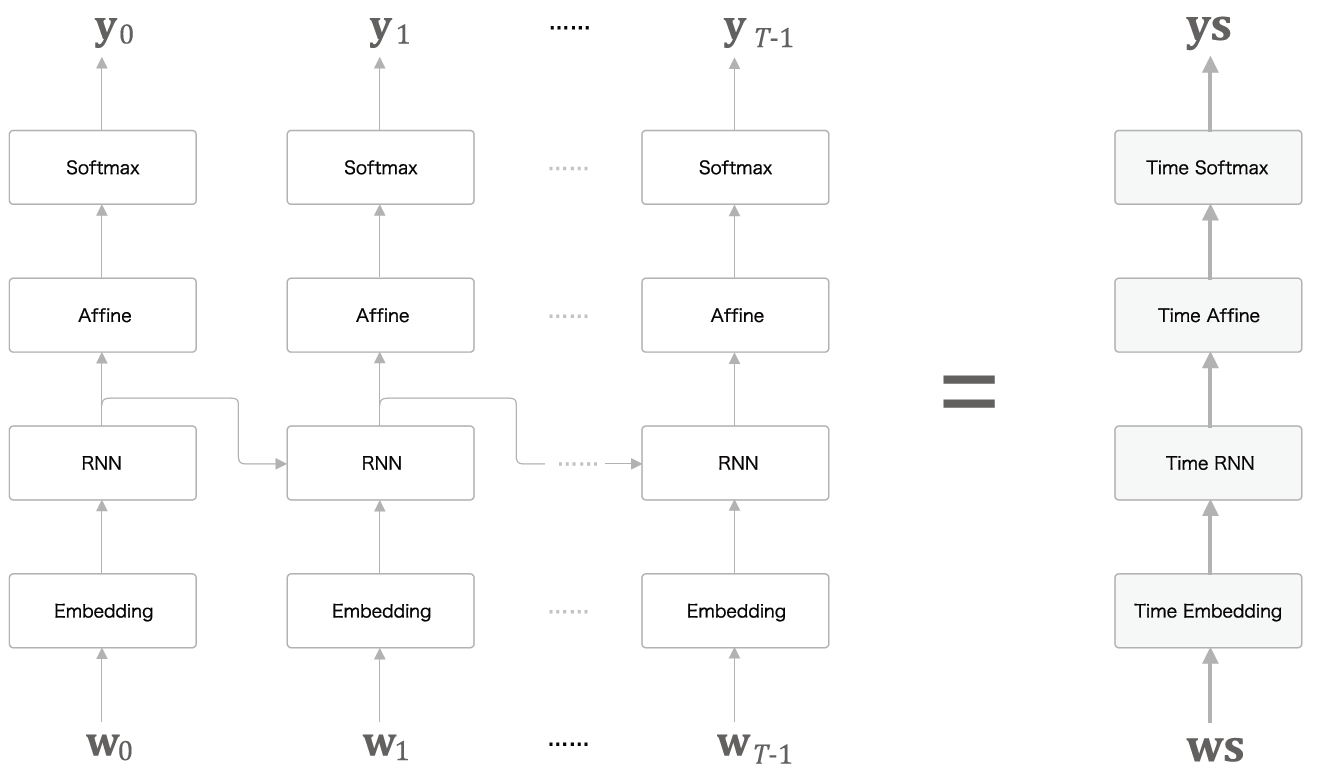
이 중 특별히 softmax with loss구현은 T개의 loss를 평균내는 방법으로 loss구현을 진행했다. 현재 다루고 있는 책 Deep Learning from scratch 2 by Saito Goki에서는 commons/time_layers.py에 각 time layer들이 구현되어있다. Affine계층은 배치처리 데이터 (N,T,D)를 (NxT,D)로 묶어 행렬곱처리하는 방식으로 구현되어있으므로 코드를 읽어보면 좋을 것 같다.
11.5 Learning & Test of RNNLM
RNNLM구현에 필요한 계층들을 모두 알게 되었으므로 이제 조립할 일만 남았다.
11.5.1 Implementing RNNLM
우선 init 메서드에서는 다음과 같이 필요한 params, layers를 정의한다.
import numpy as np
from common.time_layers import *
class SimpleRnnlm:
def __init__(self,vocab_size,wordvec_size,hidden_size):
V,D,H = self,vocab_size,wordvec_size,hidden_size # 형상
rn = np.random.randn
# Init Weights->xavier initialization
embed_W = (rn(V,D)/100).astype('f')
rnn_Wx = (rn(D,H)/np.sqrt(D)).astype('f')
rnn_Wh = (rn(H,H)/np.sqrt(H)).astype('f')
rnn_b = np.zeros(H).astype('f')
affine_W = (rn(H,V)/np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
# make layers
self.layers =[
TimeEmbedding(embed_W),
TimeRNN(rnn_Wx,rnn_Wh,rnn_b,stateful=True),
TimeAffine(affine_W,affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss() # 얘는 따로(forward에서는 이용 안하니까)
self.rnn_layer = self.layers[1]
self.params,self.grads = [],[]
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
마지막에 self.params와 grads에 모든 가중치와 기울기를 모은 것은 후에 사용할 fit() 메서드의 정의에 따른 것이다. 이제 계속해서 forward,backward구현을 보자. 그냥 layer순서대로 호출하면 된다.
def forward(self,xs,ts):
for layer in layers: # Time embedding -> TimeRNN -> TimeAffine순서대로
xs = layer.forward(xs)
loss = self.loss_layer(xs,ts)
return loss
def backward(self,dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
self.rnn_layer.reset_state()이로써 RNNLM구현이 끝났다. 이제는 실제 학습과 평가를 진행해봐야한다.
11.5.2 Perplexity
언어 모델에 대한 평가를 진행하기 전에, 우선 언어 모델의 성능 평가기준을 생각해봐야 한다. 언어 모델은 주어진 과거의 단어(정보)로부터 다음에 출현할 단어의 확률 분포를 출력한다. 이 때 언어모델의 예측 성능을 평가하는 척도로 퍼플렉서티perplexity,혼란도를 자주 이용한다.
퍼플렉서티는 간단히 말하면 확률의 역수다. 예를 들어 예측해야할 값이 "say"일 때 우리의 모델이 "say"가 출현할 확률을 0.8로 출력하면 퍼플렉서티는 1/0.8=1.25가 된다. 이 값은 타깃의 확률을 높게 추론할수록 작아지는 값으로, 작을수록 우리의 모델이 추론을 잘 한다는 것을 알 수 있다. 이 값은 정보이론 분야에서 기하평균 분기수로도 부르는데, 이는 직관적으로 퍼플렉서티는 가능한 분기수로 해석될 수 있기 때문이다. 예를 들어 퍼플렉서티가 5이면 가능한 분기수를 5개정도로 좁혔다는 의미, 1.25정도면 가능한 분기수를 1.25개정도로 좁혔다고 해석 가능하다.
상기 설명은 데이터가 한개일 때 퍼플렉서티의 정의이므로 데이터가 여러개인 경우의 퍼플렉서티도 정의해야한다. 데이터가 여러개일 때는 다음 공식에 따라 퍼플렉시티를 계산한다. t는 one-hot vector고 y는 확률분포벡터다.
$$
L=-\frac{1}{N}\sum_{n}{\sum_{k}{t_{nk}\log{y_{nk}}}} \
,perplexity=e^L
$$
식이 복잡해보이지만 천천히 생각해보면,L은 결국 신경망의 손실과 같은 값이며 다음의 과정에 따라 계산된 것이다.
- 정답 레이블에 해당하는 확률 출력에 log를 씌운 것을 다 더한다.
- 데이터의 수로 나누어 평균낸다
- 로그 씌운다.
그리고 이 식에도 확률의 역수, 분기 수, 선택사항의 수 같은 개념이 들어가있다고 하는데, 왜 그런지 수학적인 이유는 모르겠다..
11.5.3 Testing RNNLM
PTB 데이터셋의 처음 1000개 단어에 대해서만 학습을 진행하는 RNNLM코드를 작성하자. Truncated BPTT방식이고 주석을 천천히 읽어보자.
# TRUNCATED BPTT
import sys
sys.path.append('..')
import matplotlib.pyplot as plt
import numpy as np
from common.optimizer import SGD
from dataset import ptb
from simple_rnnlm import SimpleRnnlm
# 하이퍼 파라미터 설정
batch_size = 10 # 한 번에 10개의 데이터씩 본다.
wordvec_size = 100 # wordvec은 size 100의 vector로 표현한다.
hidden_size = 100 # RNN 은닉 상태 벡터의 원소 수
time_size = 5 # Truncated BPTT가 한 번에 펼치는 시간 크기
lr = 0.1 # learning rate of SGD
max_epoch = 100 # 전체 데이터를 몇 번 볼것인가?.. 전체 데이터를 총 100번 본다.
corpus,word_to_id,id_to_word = ptb.load_data('train') # data load
corpus_size = 1000 # PTB의 말뭉치 중 1000개만 보기로 함.
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus)+1) # max_id +1 하면 vocab의 수가 나오는 것 맞지.
xs = corpus[:-1] # 입력->마지막원소는 입력 필요X
ts = corpus[1:] # 출력
data_size = len(xs) # 999
print("말뭉치 크기: %d, 어휘수: %d"%(corpus_size,vocab_size))
# 학습 시 사용하는 변수
max_iters = data_size//(batch_size*time_size) # 999//(10*5)
time_idx,total_loss,loss_count=0,0,0
ppl_list = [] # perplexity list
# 모델 생성
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
# 준비 끝, 본격적 학습 시작
# 1. 각 미니배치에서 샘플을 읽기 시작할 위치를 계산
jump = (corpus_size-1)//batch_size # 999//10 = 99
offsets = [i*jump for i in range(batch_size)] # 99,198,..이 각 미니배치에서의 시작 위치가 된다.
print(offsets) # DEBUG CODE
for epoch in range(max_epoch): # epoch 변수는 쓸필요 X
for iter in range(max_iters):
print("iter:",iter) # DEBUG CODE
# 2. 미니배치 획득
batch_x = np.empty((batch_size,time_size),dtype='i')
batch_t = np.empty((batch_size,time_size),dtype='i')
idx = np.empty((batch_size,time_size),dtype='i')
for t in range(time_size):
#print(time_idx)
for i,offset in enumerate(offsets):
# 10x5의 batch를 만듦.
idx[i,t]=((offset+time_idx)%data_size)
batch_x[i,t]=xs[(offset+time_idx)%data_size]
batch_t[i,t]=ts[(offset+time_idx)%data_size]
time_idx += 1
# 기울기를 구해서 매개변수 갱신
print(idx)
loss = model.forward(batch_x,batch_t)
model.backward()
optimizer.update(model.params,model.grads)
total_loss += loss
loss_count += 1
# 에폭마다 퍼플렉서티 평가
ppl = np.exp(total_loss/loss_count)
print('|에폭 %d, 퍼플렉서티 %.2f'%(epoch+1,ppl))
ppl_list.append(float(ppl))
total_loss,total_count = 0,0
Truncated BPTT가 한 번에 펼치는 시간 크기는 5, 그 5개를 10개씩 각각 다른 위치에서 본다. 즉, 한 번의 수행에 5x10의 데이터를 보게 된다. 어떤 순서로 데이터를 보게 되는지 헷갈려서 디버깅을 해봤다. 각 iter에서 보는 index는 다음과 같다. 첫 epoch의 19번째 iter(iter: 18)에서 끝나면서 985번 데이터까지만 보게 되는데, 그것을 반영해 다음의 epoch iter0에서는 나머지 15개의 데이터도 보는 것을 확인할 수 있다.
iter: 0
[[ 0 1 2 3 4]
[ 99 100 101 102 103]
[198 199 200 201 202]
[297 298 299 300 301]
[396 397 398 399 400]
[495 496 497 498 499]
[594 595 596 597 598]
[693 694 695 696 697]
[792 793 794 795 796]
[891 892 893 894 895]]
iter: 1
[[ 5 6 7 8 9]
[104 105 106 107 108]
[203 204 205 206 207]
[302 303 304 305 306]
[401 402 403 404 405]
[500 501 502 503 504]
[599 600 601 602 603]
[698 699 700 701 702]
[797 798 799 800 801]
[896 897 898 899 900]]
iter: 2
[[ 10 11 12 13 14]
[109 110 111 112 113]
[208 209 210 211 212]
[307 308 309 310 311]
[406 407 408 409 410]
[505 506 507 508 509]
[604 605 606 607 608]
[703 704 705 706 707]
[802 803 804 805 806]
[901 902 903 904 905]]
iter: 3
[[ 15 16 17 18 19]
[114 115 116 117 118]
[213 214 215 216 217]
[312 313 314 315 316]
[411 412 413 414 415]
[510 511 512 513 514]
[609 610 611 612 613]
[708 709 710 711 712]
[807 808 809 810 811]
[906 907 908 909 910]]
.........생략.............
iter: 18
[[ 90 91 92 93 94]
[189 190 191 192 193]
[288 289 290 291 292]
[387 388 389 390 391]
[486 487 488 489 490]
[585 586 587 588 589]
[684 685 686 687 688]
[783 784 785 786 787]
[882 883 884 885 886]
[981 982 983 984 985]]
|에폭 1, 퍼플렉서티 404.08
iter: 0
[[ 95 96 97 98 99]
[194 195 196 197 198]
[293 294 295 296 297]
[392 393 394 395 396]
[491 492 493 494 495]
[590 591 592 593 594]
[689 690 691 692 693]
[788 789 790 791 792]
[887 888 889 890 891]
[986 987 988 989 990]]
iter: 1
[[100 101 102 103 104]
[199 200 201 202 203]
[298 299 300 301 302]
[397 398 399 400 401]
[496 497 498 499 500]
[595 596 597 598 599]
[694 695 696 697 698]
[793 794 795 796 797]
[892 893 894 895 896]
[991 992 993 994 995]]
iter: 2
[[105 106 107 108 109]
[204 205 206 207 208]
[303 304 305 306 307]
[402 403 404 405 406]
[501 502 503 504 505]
[600 601 602 603 604]
[699 700 701 702 703]
[798 799 800 801 802]
[897 898 899 900 901]
[996 997 998 0 1]]
.........생략.............
iter: 18
[[185 186 187 188 189]
[284 285 286 287 288]
[383 384 385 386 387]
[482 483 484 485 486]
[581 582 583 584 585]
[680 681 682 683 684]
[779 780 781 782 783]
[878 879 880 881 882]
[977 978 979 980 981]
[ 77 78 79 80 81]]
|에폭 2, 퍼플렉서티 17.18
iter: 0그리고 perplexity추이를 기록해보면 다음 <그림21>과 같다.

학습이 잘 진행되는 것을 확인할 수 있다. 그러나 RNNLM은 말뭉치의 크기가 커지면 잘 작동하지 않아서 다른 모델을 적용해야한다.
Reference: Deep Learning from scratch 2 by Saito Goki
All codes on: https://github.com/WegraLee/deep-learning-from-scratch-2
'머신러닝' 카테고리의 다른 글
| [ML/NLP] 10. Improving Word2Vec (0) | 2020.09.05 |
|---|---|
| [ML/NLP] 9. Simple Word2vec (0) | 2020.08.27 |
| [ML/NLP] 8. Distributional Representation of Words (0) | 2020.08.25 |
| [ML] 7. Convolutional Neural Network (0) | 2020.08.22 |
| [ML] 6. Back Propagation (2) | 2020.08.08 |
- Total
- Today
- Yesterday
- CS
- CNN
- gradient descent
- 머신 러닝
- 영상구조
- 인덱스 이미지
- 사진구조
- 순환 신경망
- 신경망
- Neural Network
- 이산 신호
- 자연어 처리
- 머신러닝
- Logistic Regression
- 컴퓨터 과학
- 매트랩
- 매트랩 함수
- RGB이미지
- 영상처리
- rnn
- 컴퓨터과학
- 밑바닥부터 시작하는 딥러닝
- 이미지
- ML
- NLP
- 연속 신호
- 이미지처리
- 신호 및 시스템
- Andrew ng
- 딥러닝
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
