티스토리 뷰
1.3 Exponentials & Sinusoidal Signals
1.3.1 Continuous-time complex exponential & sinusoidal signals
-1. Complex exponential
complex exponential은 다음과 같이 쓸 수 있는 함수를 말한다.
$$
x(t)=Ce^{at}, \quad c,a \in complex
$$
이 때 x(t)는 a와 C가 real인가 imaginary인가에 의해 다양한 함수 꼴이 된다.
1) a,C are Real
이 때는 아래 <그림1>과 같이 단순 exponential로 다음과 같은 그래프가 그려지는 함수이다.
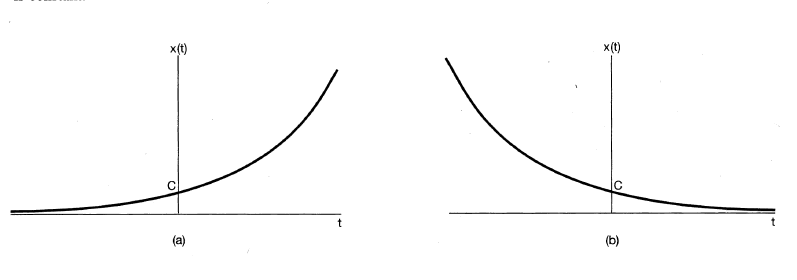
2) a is pure imaginary & C=1(for simplicity)
그러면 x(t)는 a를 jwt로 쓸 때 오일러 변환을 사용하면 다음과 같이 표현된다.
$$
x(t)=e^{j\omega t}=cos(2\pi f_{0}t) + jsin(2\pi f_{0}t)
$$
이 때 이 x(t)를 물리적으로 해석해볼 수 있다. 식의 cos부분과 sin부분은 각각 단위원 위의 x좌표, y좌표가 된다. 따라서 다음<그림2>와 같은 복소평면 위의 단위원에서 t의 증가에 의해 화살표 방향으로 움직이는 점을 생각해볼 수 있는데, 따라서 주어진 exponential function을 Rotation으로 볼 수 있다. 또한 f0가 const이므로 그 각속도는 고정된 회전이 된다.
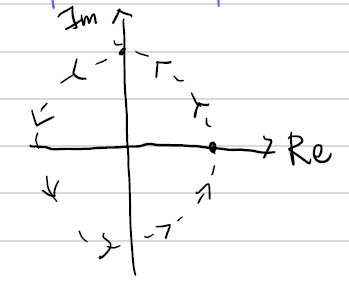
이 때 x(t)의 실수부와 허수부는 각각이 단위원 위의 점에서의 Real axis, Im axis로의 projection이니까 실수부와 허수부의 그래프가 cos, sin이 나오는 것이 매우 당연하다는 것도 생각해볼 수 있다.
$$
Re{ x(t) }=cos(2\pi f_{0}t),\quad Im{ x(t) }=sin(2\pi f_{0}t)
$$
-Periodicity of exponential
이 때 exponential의 주기성에 대해 따져볼 것인데 우선은 2)의 경우에 한해 생각해보자. 그러면 주기 T에 대해 x(t)는 다음 성질을 만족해야한다.
$$
x(t)=x(t+T),\quad \therefore e^{jwt}=e^{jw(t+T)}, \quad \therefore e^{j2\pi f_{0}T}=1
$$
따라서 마지막 식에서 주어진 오일러 식의 각이 2_pi의 정수배일때만 그 실수부가 1이 될 수 있으므로 다음 관계가 성립한다.
$$
2\pi f_{0}T=2\pi n, \quad n \in Z \quad and \quad n \neq 0
$$
그런데, 생각해보면 하나의 함수에 대해서도 *_주기는 여러개가 나올 수 있다.** 예를 들어 그냥 sin함수같은 경우에도 2pi를 주기라고 말하지만 4pi, 6pi, 8pi도 수학적인 주기다. 따라서 우리가 공부하고있는 exponential에 대해서 여러개의 주기 중 특별한 주기를 하나 뽑아서 fundamental period라는 개념을 정의한다.
이 때 fundamental period는 smallest positive T이며 수학적으로 밑과 같이 쓸수있다. 추가적으로 이 fundamental period에 대응하는 fundamental frequency도 정의할 수 있다.
-fundamental period and fundamental frequency
$$
T_{fund}=\frac{1}{f_{0}},\quad f_{fund}=\frac{1}{T_{fund}}=f_{0}
$$
3) a & C are both complex
이제 가장 일반적인 exponential의 form 해석을 살펴보자. 이 때 a와 C는 complex이므로 다음과 같이 분해할 수 있다. a는 지수에 들어갈 수이므로 그냥 분해했다.
$$
a=\gamma + j2\pi f_{0},\quad C=|C|e^{j\theta}
$$
그러면 주어진 x(t)를 다음과 같이 실수부/허수부로 잘라서 정리해볼 수 있다.
$$
x(t)=Ce^{at}=|C|e^{\gamma t + j2\pi f_{0} t+j\theta}=|C|e^{\gamma t}\times e^{j(2\pi f_{0}t+\theta)}
$$
이 함수도 t에 대한 함수로 생각해볼 수 있는데 정리한 식에서 곱셈기호 앞의 부분은 실수이고 뒤의 부분은 허수부분이므로
- 앞의 부분은 회전하는 원의 반지름을 결정하는 부분
- 뒤의 부분은 원의 회전각을 결정하는 부분
으로 해석해볼 수 있다. 따라서 t, Re, Im축을 모두 결정하여 그려보면 대략 밑의 <그림3>과 같은 그래프가 될 것이다.(대략적인 경향임, gamma가 음수면 반지름은 늘어나는 것이 아니라 줄어들 것)
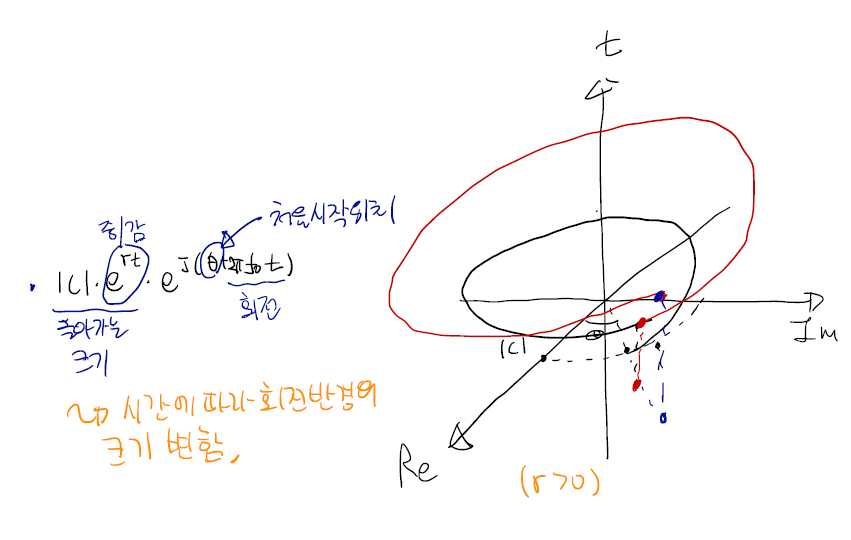
-2. Sinusoidal
sinusoidal signal은 일반적으로 다음과 같이 표현할 수 있는 함수다.
$$
x(t)=Acos(2\pi f_{0}t+\phi)
$$
이 때 periodicity는 sin함수이므로 너무 명확하고 따라서 fundamental period까지 단숨에 정의된다.
-periodicity of sinusoidal
$$
T_{fund}=\frac{1}{f_{0}}
$$
이 때 t가 일반적인 sec단위로 주어진다면 다른 상수들의 unit은 다음과 같이 주어진다.
-Units of variables/constants
$$
t:sec \quad \phi:radian\quad \omega_{0}: radian/sec \quad f_{0}:cycle/sec \quad or \quad Hz
$$
또한 (N수생이)고등학교 때 배운 삼각함수 공식과 오일러 등식을 이용하면 주어진 x(t)를 밑과 같이 변형할 수 있다.
$$
x(t)=Acos(2\pi f_{0}t+\phi)=\frac{A}{2}{e^{j\phi}e^{j2\pi f_{0}t} +e^{-j\phi}e^{-j2\pi f_{0}t}}
$$
이 때 마지막 덧셈 항에서 앞의 항은 counter clock-wise로 회전하고 뒤의 항은 clock-wise로 회전하므로 다음<그림4>와 같은 두 회전의 합으로 볼 수 있다. 편의를 위해 phi=0으로 두었다. phi 가 0이 아니면 출발 지점이 달라질 뿐이다.
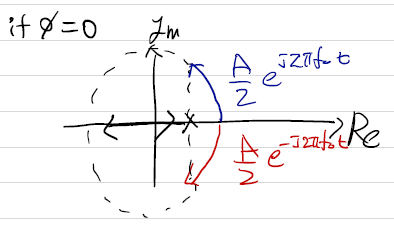
-3. Energy & Power of periodic signals(exp & sin)
위에서 살펴본 exponential과 sinusoidal의 periodic function은 주기함수의 power와 Energy는 다음 성질을 만족한다.
- finite Power
- infinite Energy
사실 이는 직관적으로 당연한 것이, T만큼의 구간에서만 적분한 Energy는 finite할 것이고 따라서 T구간에서 구한 Energy는 상수고, 그것을 T로 나누면 finite한 수가 나온다. power는 이런 (에너지 적분값)/(구간길이)를 전구간에 대해서 하게 되는 것이므로 똑같은 과정이 반복되어 finite한 값이 나오게 된다. 또한 이런 finite한 값에 구간의 길이를 곱한 것이 Energy가 되므로 Energy는 infinite하게 된다. 이 말이 잘 이해가 안된다면 예제로 다음의 주어진 x(t)에 대한 power를 구하는 과정을 살펴보자.
$$
if\quad x(t)=e^{j2\pi f_{0}t},\quad P_{\infty}=\lim _{ T\rightarrow \infty }{ \frac{1}{2T} \int _{ -T }^{ T }{|e^{j2\pi f_{0}t} |}^2dt } =1
$$
P_inf를 구하는 식에서 integral값은 적분 구간이 -T
2T, -3T~3T로 늘어나도 주기성에 의해 그 값이 A,2A,3A로 적분구간에 비례하여 늘어나는 꼴이므로 항상 finite한 값이 된다.(물론 적분 구간이 T*정수 꼴이 아닐 때는 정확한 선형비례는 아닐 것이다. 하지만 적분구간이 T의 정수비례한 값일 때 위의 성질을 보인 것만으로도 finite함이 당연.)
-여기가 잘 이해되지 않는다면 원서의 18~19p넘어가는 부분 설명을 보자.
*Harmonically related complex exp.
위에서 주어진 complex exponential의 주기성을 조금 더 면밀히 활용하기 위해 Harmonically related complex exp라는 개념을 새로 정의한다. 우선 개념의 도입 필요성부터 천천히 보자.
complex exponential을 조금 더 간단하게 살펴보기 위해 x(t)를 가장 간단한 다음과 같은 함수로 정해보자.
$$
x(t)=e^{j2\pi ft}
$$
이 때 x(t)가 특정 주기 T0 을 가지기 위해서는 x(t)=x(t+T)여야 하므로 다음과 같은 식을 만족해야 한다.
$$
e^{j2\pi f_t}=e^{j2\pi f_(t+T_{0})},\quad \therefore e^{j2\pi fT_{0}}=1 \rightarrow \quad 2\pi fT_{0}=2\pi k \quad for \quad integer \quad k
$$
따라서 f 는 다음과 같은 식을 만족해야 한다.
$$
f=\frac{k}{T_{0}},k=0,\pm 1,\pm 2, ....
$$
따라서 만약 k=1일 때의f를 f0로 정의한다면 f와 f0은 다음 관계를 만족해야한다.
$$
f_{0}=\frac{1}{T_{0}},\quad \therefore f=k\times f_{0}
$$
가 된다. 따라서 이제 주어진 T0에 대해 어떤 f가 되어야 complex exponential이 주기성을 만족할 수 있는지 알게 되었다. 따라서 T0을 주기로 하는 complex exponential function의 set을 정의할 수 있다. 그것이 Harmonically related complex exp이다.
-
Definition of Harmonically related complex exp.
Def) 공통 주기 T0을 갖는 주기 exp 함수들을 모아놓은 집합이다. 만약 f0 =1/T0라 정의하면
$$
\phi_{k}(t)=e^{j2\pi kf_{0}t}
$$
-단순히 f를 kf0로 바꿔놓은 꼴이라는 점을 깨달아야 한다.
Harmonically related complex exp는 또한 basis function을 형성한다고 하는데 이에 대한 개념은 나중에 알아본다고 한다.
1.3.2 Discrete-time complex Exponential & Sinusoidal Signals
-1. Complex exponential
1.3.1에서는 Continuous time에 대해서 알아보았으니까 이제 Discrete time signal에 대해서도 알아봐야 한다. 유형을 조금 더 간단히 분류하기 위해 x(n)을 continuous time과는 조금 다르게 정해보자.
$$
x(n)=C\alpha^{n}=Ce^{\beta n}
$$
1) If C & alpha are real (Real Exponential Signal)
이 경우에는 alpha의 값에 따라 그려지는 그래프의 모양이 달라질 것이다. 아래는 그 분류이다.
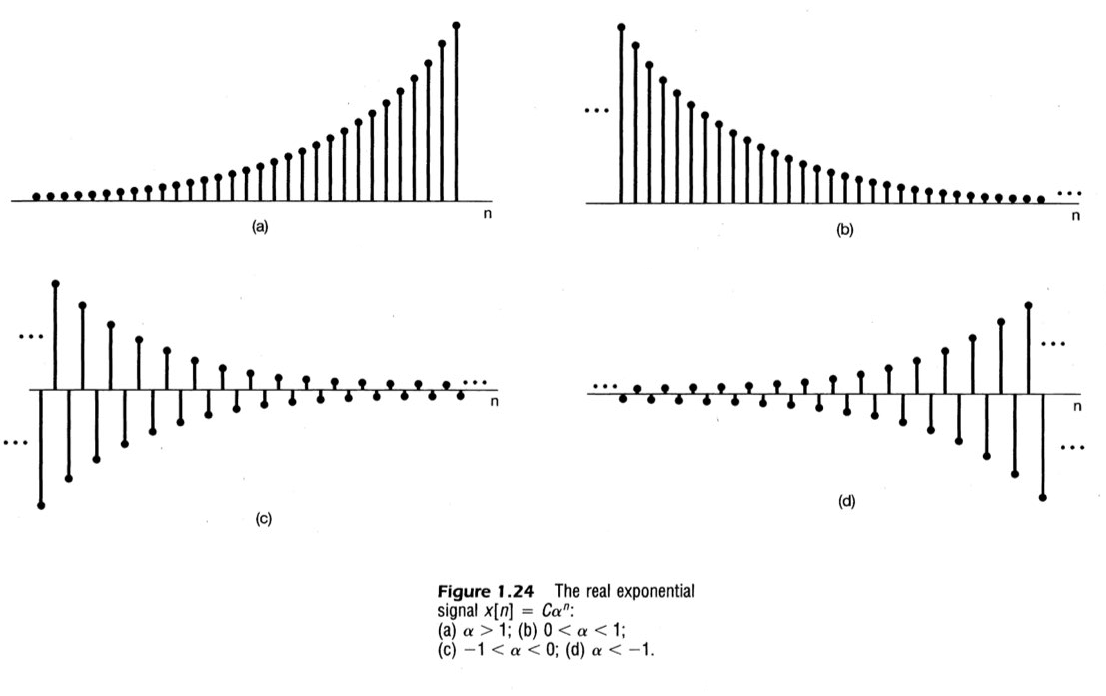
2) If C & alpha are both complex
continuous한 경우를 분석했을 때와 비슷한 IDEA로 분해한다.
$$
C=|C|e^{j\theta}, \quad \alpha = |\alpha\ |e^{j2\pi f_0}
$$
그러면 x(n)은 오일러 공식을 써서 다음과 같이 표현할 수 있다.
$$
C\alpha^{n}=|C||\alpha |^{n}e^{j(\theta+2\pi f_0)}=|C||\alpha |^{n}(cos(2\pi f_0n+\theta)+jsin(2\pi f_0n+\theta))
$$
이는 continuous time에서의 both complex 경우와 같으므로 그 경우의 그래프인 <그림3>에서 특정 점들만이 찍히는 경우로 해석할 수 있다.
-2. Sinusoidal Signal
사실 sinusoidal signal은 1-2)에서 다음과 같은 x(n)에 대해
$$
x(n)=C\alpha^{n}=Ce^{\beta n}
$$
일 때 beta가 pure imaginery인 특수한 경우로 생각할 수 있다. 왜냐하면 beta와 C를 다음과 같이 설정하면
$$
\beta = j2\pi f_o n, \quad C=|C|e^{j\theta}
$$
x(n)이 오일러 공식에 의해 다음과 같이 표현되기 때문이다.
$$
x(n)=Ce^{n}=|C|e^{j(\theta+2\pi f_0n)}=|C|(cos(\theta+2\pi f_0n)+jsin(\theta+2\pi f_0n))
$$
이는 n에 의해 회전의 크기가 변하는 1-2)와 같은 경우가 아니므로 sinusoidal이 맞다. 또한 위에서 논한 periodic의 Power와 Energy성질에 의해 Dt sinusoidal signal의 전체 구간에서의 power와 Energy는 다음을 만족한다.
- Energy is infinite
- Power is finite
그래프가 어떻게 그려지는가에 관하여는 바로 다음의 챕터 1.3.3에서 논한다.
1.3.3 Periodicity Properties of Discrete-time Complex Exponential
Ct-signal과 Dt-signal에는 많은 유사성이 있지만 몇 가지 중요한 다른 성질들이 존재한다.
Property 1: frequency
e^{jwt}는 서로 다른 두 주파수값 w에 대해 서로 다른 두 함수임이 자명하다. 그러나 Dt-signal은 이런 Ct-signal에서 몇개의 점만이 찍히는 함수이다. 따라서 주파수가 다르다고 항상 다른 함수가 되는지 의심해볼 수 있다.
임의의 정수 k에 대해 f0대신 주파수 f0+k를 넣은 것이 다음 식을 만족한다는 것을 생각해보자.
$$
e^{j2\pi (f_0+k)n}=e^{j2\pi f_0n} \times e^{j2\pi kn}, \quad \because e^{j2\pi kn} = 1 \quad for \quad integer \quad k
$$
그래서 결국 우항을 정리하면 다음 사실을 알 수 있다.
$$
e^{j2\pi (f_0+k)n}=e^{j2\pi f_0n}
$$
결국 f0대신 f0에 임의의 정수 k를 더한 값이 들어가도 동일한 함수가 된다. 따라서 결국 어떤 주파수 f0와 f0+k는 같은 주파수로 생각할 수 있다.
결론: Dt-signal에서 f0와 f0+k는 동일한 주파수다.
이제, Dt-signal에서는 Ct-signal처럼 모든 주파수가 distinct한 것이 아님을 알게되었으므로 높은 주파수, 낮은 주파수 등의 개념을 다시 생각해볼 필요가 있다. 우선 Distinct한 frequency는 오직 어떤 실수 r에 대해 r보다 크거나 같고 r+1보다 작은 구간에서만 정의될 수 있으므로 우리의 distinct한 주파수 interval은 다음과 같이 정해보자.(어떻게 정하든 상관 X)
$$
0 \le f_0 < 1
$$
그러면 이전에 Ct-signal에서 정의했던 높은 주파수, 낮은 주파수의 개념을 다음과 같은 x(n)에서 생각해보자.
$$
x(n)=e^{j2\pi f_0n}
$$
높은 주파수란 n의 변화에 따라 값의 변화가 최대한 자주 일어나는 것이다. 예를 들어 f0=0.5 인 경우를 생각해보자. 그러면 x(n)은 (-1)^n이 되어 n이 변할때마다 1,-1을 왔다갔다 할것이다. 이 값이 highest frequency이다.
다른 경우로 f0=0인 경우를 생각해보자. 그러면 x(n)=1로 n에 의해 값이 변하지 않고 일정한 값만이 찍힐 것이다. 따라서 이것이 lowest frequency가 된다.
적당한 주파수일 때는 함수의 Re축과 Im축에 찍히는 값이 삼각함수의 일부가 될 것이다. 다음 <그림6>은 그 예시들이다. 차례대로 적당한 주파수, 낮은 주파수, 높은 주파수의 n에 따른 Re축 그래프이다.
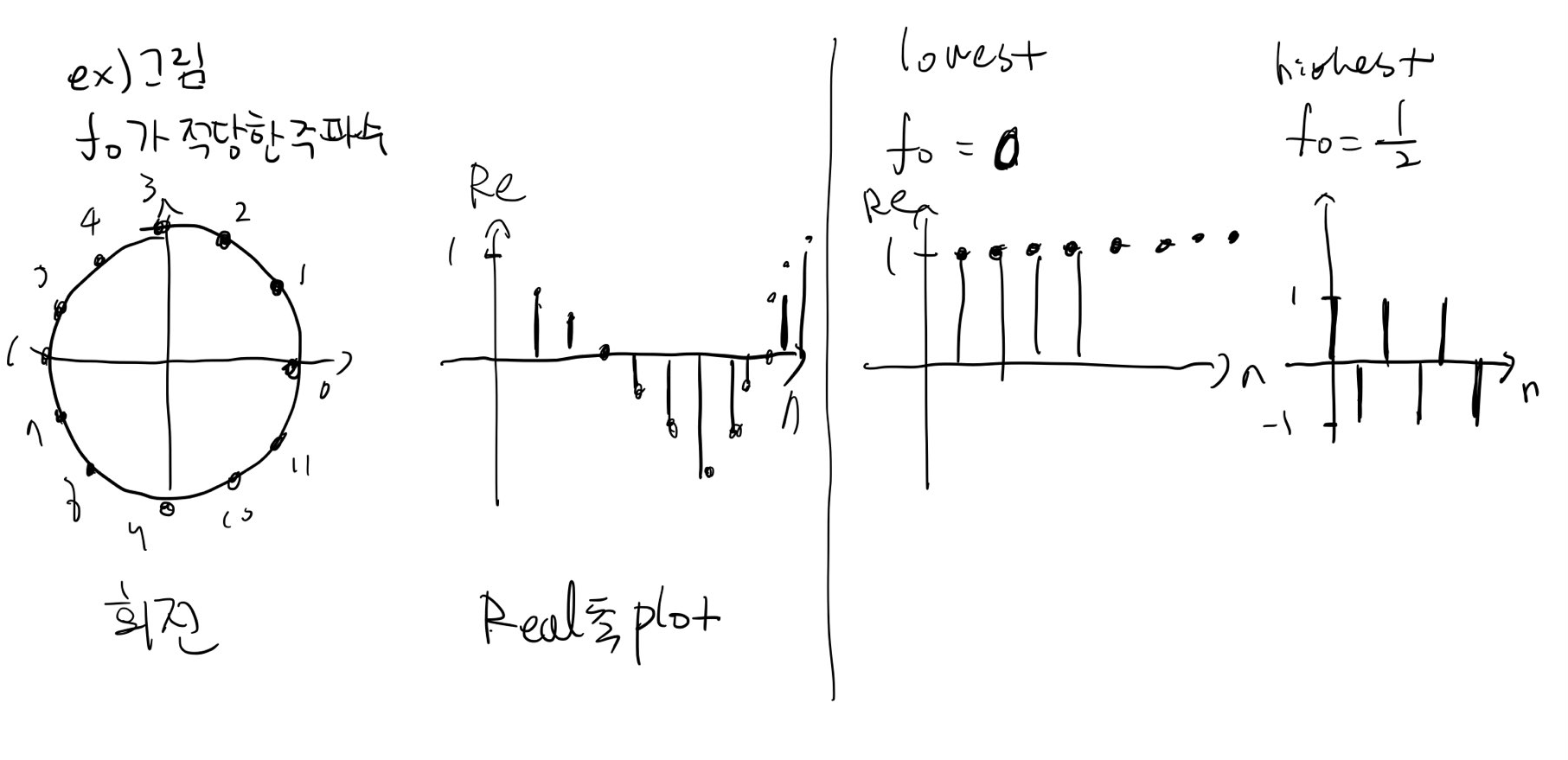
property 2: periodicity
Ct-signal에서는 e^{jwt}는 임의의 w에 대해 반드시 주기함수였다.(=반드시 그 주기를 찾을 수 있었다.) 그러면 Dt-signal에서는 이런 Periodicity가 어떤 차이점을 보일까?
periodic이 되기 위해서는 임의의 주기인 자연수 N에 대해 다음 식을 만족해야 한다.
$$
e^{j2\pi f_0n}=e^{j2\pi f_0(n+N)},i.e.\quad e^{j2\pi f_0N}=1
$$
따라서 f0는 정수 m에 대해 다음을 만족해야 한다.
$$
f_oN=m,i.e.\quad f_o= \frac{m}{N}
$$
결론: 따라서 f0가 유리수가 아니면 주기성이 없다는 것을 알 수 있다.
결론을 다시 말하면 f0가 다음과 같이 유리수로 나타날 때
$$
f_o= \frac{m}{N}
$$
그 주기가 N이 되는 것을 뜻한다. (물론 약분이 되는 유리수이면 N의 약수 주기를 가질 수 있다. 그렇게 되어도 방금 말한 결론은 성립한다.)
Property 3: fundamental period
Ct-signal에서는 가능한 period가 여러개이므로 그 중 smallest positive T를 fundamental period로 정하였다. Dt-signal에서도 smallest positive한 주기를 fundamental period로 동일하게 가져오기 위해 논의를 다시 진행해야할 필요가 있다.
상기 property 2로부터
$$
f_0 = \frac {m}{N}
$$
임을 알 수 있다. 이 때 m과 N에 common factor가 없어서 약분이 불가능한 서로소이면 fundamental period를 다음과 같이 정의할 수 있다.
$$
N_{fund} =\frac{m}{f_0}=N
$$
이 때 Ct-signal에서의 fundatmental period를 떠올려보면 다음과 같다.
$$
T_{fund}= \frac{1}{f_0}
$$
이제 N_fund와 T_fund를 비교해보면 다음과 같고
$$
N_{fund}=m\times T_{fund}
$$
이 사실을 다음과 같은 중요한 결론으로 정리할 수 있다!
결론: Dt-signal에서의 fundamental period는 동일한 함수의 Ct-signal의 fundamental period보다 m배 길다.
이것을 직관적으로 이해하기 위해 다음과 같은 예제를 떠올려볼 수 있다.
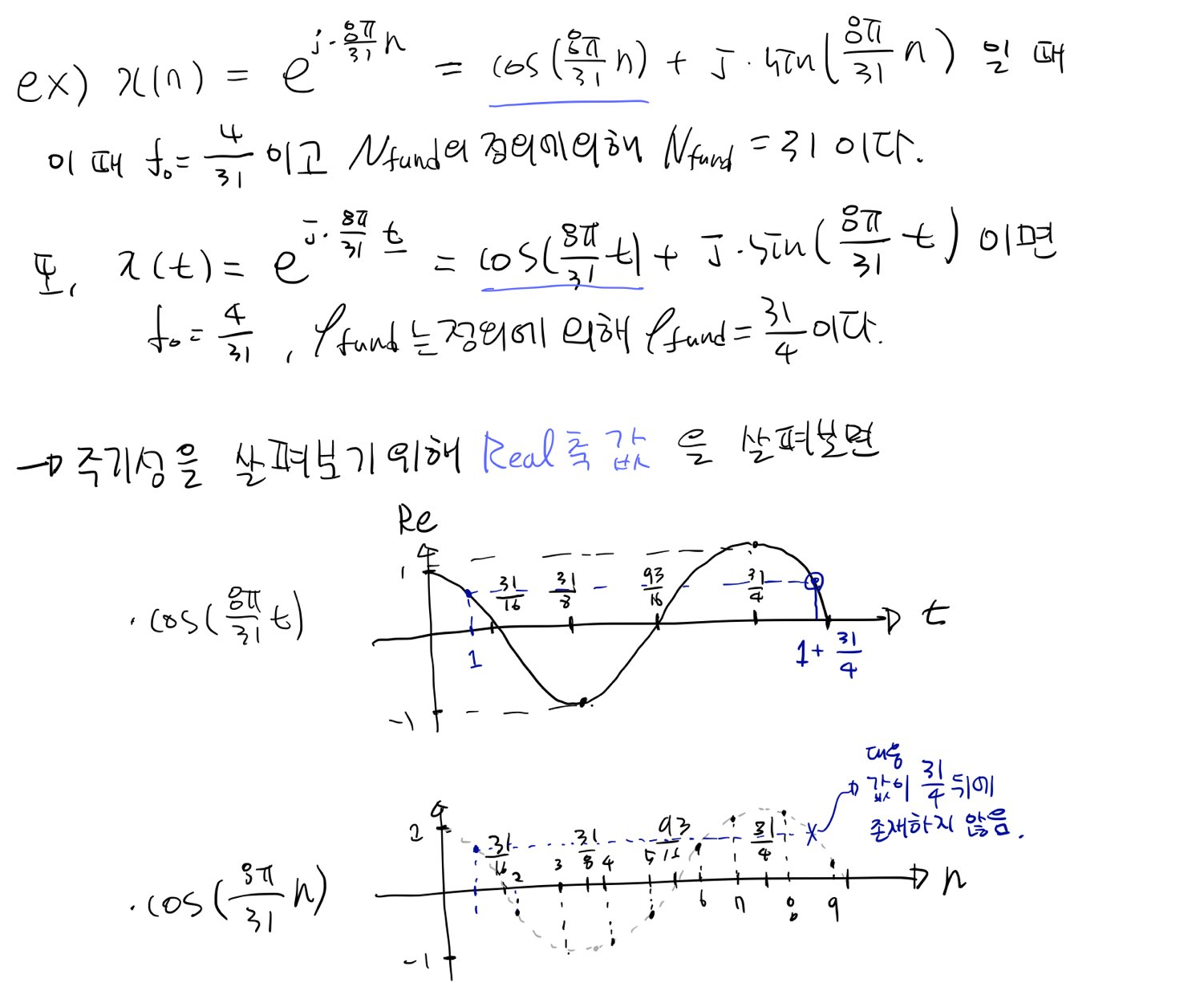
-Harmonically related exp in Dt-signal
이제 Ct-signal에서 정의했던 개념을 Dt-signal에 대해서도 정의해볼 수 있다. 우선 Ct-signal에서 Harmonically related exp가 어떤 개념이었는지 생각해보자. Ct-signal에서 그 개념은 주어진 주기 T0에 대해 T0를 주기로 갖는 모든 exp를 모아놓은 set을 얘기했다. 이런 개념이 Dt-signal에도 확장된다.
논의를 위의 f0로부터 진행시켜보자. f0가 다음과 같은 기약분수일 때
$$
f_0=\frac{m}{N},\quad
$$
fundamental period, 즉 가장 짧은 양수 주기는 다음과 같이 정의되었다.
$$
N_{fund}=N
$$
이 때 생각해보면 정수 k에 대해 다음과 같이 정의되는 특정 주파수 f는 그 주기가 N을 만족함을 알 수 있는데,
$$
f=\frac{k}{N}
$$
왜냐하면 f는 무조건 다음과 같은 유리수이기 때문이다.
- f가 기약분수인 경우: fundamental period가 N이므로 그 주기가 N
- f가 기약분수가 아닌 경우: fundamental period가 N의 약수->N도 하나의 주기가 됨
따라서 주어지는 N에 대해 N을 주기로 하는 Dt-exp를 모아놓은 set을 다음과 같이 정의할 수 있다.
$$
\phi_k[n]=e^{j2\pi(\frac{k}{N})n}
$$
이 식은 단순히 f를 k/N으로 바꿔놓은 꼴이라는 것을 이해해야 한다.
그리고, Ct-signal에서는 f가 다른 모든 exp가 distinct했기 때문에 harmonically related exp의 원소 개수가 infinite했다. 그러나 Dt-signal에서는 distinct한 주파수의 range가 제한되어 있었다. 따라서 이 set의 원소 개수를 다시 생각해봐야할 필요가 있는데, k대신 k+N이 들어가는 순간 식은 다음과 같이 변한다.
$$
\phi_{k+N}[n]=e^{j2\pi(\frac{k}{N})n+j2\pi n}=e^{j2\pi(\frac{k}{N})n}=\phi_k[n]
$$
따라서 k가 0부터 N-1까지만 distinct한 함수들이 나오므로 set의 원소 개수는 N개임을 알 수 있다.
'신호 및 시스템' 카테고리의 다른 글
| [신호] 1.4 The Unit Impulse & Unit Step Functions //단위 임펄스 함수 & 단위 계단 함수 (0) | 2020.03.21 |
|---|---|
| [신호] 1.2 transformations of independent variables (0) | 2020.03.15 |
| [신호] 1.1 Continuous-time & Discrete time signal //연속 시간& 이산 시간 신호 (0) | 2020.03.15 |
| [신호] 1. 개요-신호와 관련된 개념 //신호, 주파수, 샘플링 (0) | 2020.03.15 |
| 0. 카테고리 목적 (0) | 2020.03.14 |
- Total
- Today
- Yesterday
- 인덱스 이미지
- 매트랩
- gradient descent
- 컴퓨터 과학
- 이미지
- 연속 신호
- Neural Network
- 순환 신경망
- 신경망
- 신호 및 시스템
- 이산 신호
- CS
- 영상구조
- ML
- 매트랩 함수
- rnn
- 머신 러닝
- 머신러닝
- 컴퓨터과학
- 딥러닝
- RGB이미지
- CNN
- Logistic Regression
- 이미지처리
- Andrew ng
- 밑바닥부터 시작하는 딥러닝
- NLP
- 사진구조
- 영상처리
- 자연어 처리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
