티스토리 뷰
[신호] 1.4 The Unit Impulse & Unit Step Functions //단위 임펄스 함수 & 단위 계단 함수
hezma 2020. 3. 21. 16:501.4 The Unit Impulse & Unit Step Functions
공학 분야에서 많이 사용되는 genaralize function인 unit impulse와 unit step function을 Dt-signal과 Ct-signal에서 각각 정의한다.
1.4.1 The Discrete-time Unit Impulse and Unit step sequences
(1) DT unit Impulse의 정의
DT unit impulse의 정의는 아래와 같고, kronecker delta라는 이름이 있다.
$$
\delta (n)=0 (n\neq 0),\quad 1(n=0)
$$
이를 그래프에 표현해보면 <그림1>과 같이 생겼다.
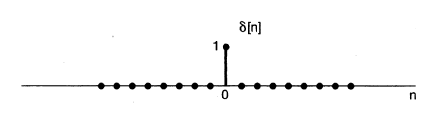
(2) DT unit step sequence의 정의
DT unit step의 정의는 아래와 같다.
$$
u(n)=0(n<0), \quad 1(n\ge0)
$$
이를 그래프에 표현해보면 <그림2>와 같이 생겼다.

(3) Property of unit impulse & unit step
1) Relation between Unit impulse & Unit step in Dt.
-> unit impulse를 unit step function을 이용하여 어떻게 표현할 수 있을까?
정답은 u(n)에서 u(n)을 오른쪽으로 한 칸 만큼 이동시킨 함수를 빼주면 된다. 그러면 n=0에서의 1만 남고 나머지는 다 0이 된다. 이를 식으로 표현해보면 다음과 같다.
$$
\delta (n)= u(n)-u(n-1)
$$
그러면 반대의 경우도 가능하지 않을까? step sequence를 impulse로 표현하려면 어떻게 하면 될까?
impulse는 1이 여러개고 step은 1이 딱 하나니까 1을 여러개 이동시켜서 만들어야 하지 않을까? 이 아이디어를 사용해서 step function을 impulse로 나타내보면 다음과 같다.
$$
u(n)=\sum _{ k=0 }^{\infty }{\delta (n-k)}=\sum _{ m=-\infty }^{n }{\delta (m)}
$$
두 번째 표현인 delta(m)은 첫 표현의 식을 치환한 꼴이지만, 조금 직관적으로 이해해보면 다음의 식에서
$$
u(n)=\sum _{ m=-\infty }^{n }{\delta (m)}
$$
- n>0->0
- n=0->1
- n>0->1(왜냐하면 1의 값은 u(0)인 거에서 하나밖에 안 나오니까)
2) equation with Dt-signal x(n)
Dt-signal인 x(n)과 delta(n)은 다음 식을 만족한다.
$$
x(n)\delta (n)=x(0)\delta(n)
$$
왜냐하면 어차피 delta(n)은 n=0에서만 그 값이 활성화되기 때문이다.
이 때 이 식을 조금 더 일반적으로 이용해보기 위해 n=a에서만 값이 활성화되는 함수를 생각해보면, delta(n-a)일 것이다. 따라서 이 평행이동 버전을 다음과 같이 정리해볼 수 있다.
$$
x(n)\delta (n-a)=x(a)\delta (n-a)
$$
이 식이 성립하는 이유도 어차피 delta(n-a)는 n=a에서만 그 값이 활성화 되기 때문이라는 것을 알 수 있다.
1.4.2 The Continuous-time Unit Impulse and Unit step sequences
(1) Ct unit impulse의 정의 //Dirac's Delta
ct unit impulse는 그 정의가 다음 두 조건을 모두 만족해야 한다.
$$
\delta (t)=\infty (t=0),\quad0(t \neq 0) \quad \And \quad \int _{ -\infty }^{ \infty }{f(t)dt } =1
$$
그림으로 표현하면 다음<그림3>과 같다. 위로 올라가는 화살표 1은 amplitude를 말하는 것이 아니라 area가 1이라는 것을 표현하는 부호다. 또한 이 (genaralized)함수를 Dirac's delta라고도 한다.(엄밀히 말하면 함수가 아니다.)

(2) Ct unit step의 정의
Dt unit step이랑 거의 비슷하게 정의된다.
$$
u(t)=0(t<0),\quad 1(t>0)
$$
주의해야 할 점은 t=0에서 정의되지 않는다는 것이다. 이를 표현한 다음 <그림4>를 보자.

(3) Property
1) Relation between Unit impulse & Unit step in Ct.
unit impulse의 적분 값이 1이라는 것을 아이디어로 다음과 같이 unit step을 이용하여 정의할 수 있다.
$$
\delta (t)=\frac{du(t)}{dt}
$$
또한 아까 Dt에서의 idea를 이용하면 u(t)도 delta를 이용해 정의할 수 있다.
$$
u(t)= \int _{ 0 }^{ \infty }{\delta (t-\tau )d\tau }=\int _{ -\infty }^{t}{\delta (\tau )d\tau }
$$
2) Equation with Ct-signal x(t)
t=0에서만 impulse의 값이 활성화 대는 것을 생각해보면 다음과 같이 쓸 수 있다.
$$
x(t)\delta (t)=x(0)\delta (t)
$$
t=a에서만 impulse의 값을 활성화하게 하여 다음과 같이 변형된 식을 쓸 수도 있다.
$$
x(t)\delta (t-a)=x(a)\delta (t-a)
$$
'신호 및 시스템' 카테고리의 다른 글
| [신호] 1.3 Exponential & Sinusoidal signals //복소 지수 신호와 삼각 신호 (0) | 2020.03.17 |
|---|---|
| [신호] 1.2 transformations of independent variables (0) | 2020.03.15 |
| [신호] 1.1 Continuous-time & Discrete time signal //연속 시간& 이산 시간 신호 (0) | 2020.03.15 |
| [신호] 1. 개요-신호와 관련된 개념 //신호, 주파수, 샘플링 (0) | 2020.03.15 |
| 0. 카테고리 목적 (0) | 2020.03.14 |
- Total
- Today
- Yesterday
- 자연어 처리
- 인덱스 이미지
- Logistic Regression
- 이미지처리
- ML
- 매트랩 함수
- NLP
- 순환 신경망
- rnn
- 이산 신호
- 사진구조
- 이미지
- 영상구조
- Neural Network
- 머신 러닝
- 신호 및 시스템
- gradient descent
- 컴퓨터과학
- CS
- 신경망
- 딥러닝
- 매트랩
- 연속 신호
- 머신러닝
- RGB이미지
- 영상처리
- 컴퓨터 과학
- Andrew ng
- CNN
- 밑바닥부터 시작하는 딥러닝
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
